题目内容
 (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=| 2 |
(1)设O是线段BD的中点,求证:C1O∥平面AB1D1;
(2)求直线AB1与平面ADD1所成的角.
分析:(1)取B1D1的中点E,连接AC,AE,C1E,先证明四边形C1EAO为平行四边形,再利用线面平行的判定定理证明C1O∥平面AB1D1即可;
(2)补图构成直平行六面体ABCD-A1B1C1D1,作B1F⊥A1D1于F,先利用线面垂直的判定定理证明B1F⊥平面ADD1,从而找到线面角的平面角∠B1AF,最后在直角三角形中计算此角即可
(2)补图构成直平行六面体ABCD-A1B1C1D1,作B1F⊥A1D1于F,先利用线面垂直的判定定理证明B1F⊥平面ADD1,从而找到线面角的平面角∠B1AF,最后在直角三角形中计算此角即可
解答:解:(1)取B1D1的中点E,连接AC,AE,C1E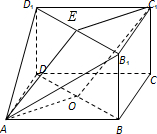
∵C1E∥CO,C1E=CO,CO=OA
∴C1E∥OA,C1E=AO
∴四边形C1EAO为平行四边形,
∴C1O∥EA,又EA?平面AB1D1;
∴C1O∥平面AB1D1;
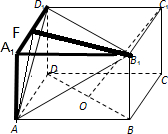
(2)如图:补图构成平行六面体ABCD-A1B1C1D1,作B1F⊥A1D1于F,
连AF,∵B1F⊥DD1,DD1∩A1D1=D1,
∴B1F⊥平面ADD1,
∴∠B1AF为直线AB1与平面ADD1所成的角
在△B1AF中可计算出 AB1=
=
,B1F=
×sin60°=
∴在△B1AF中 sin∠B1AF=
=
∴直线AB1与平面ADD1所成的角为
.

∵C1E∥CO,C1E=CO,CO=OA
∴C1E∥OA,C1E=AO
∴四边形C1EAO为平行四边形,
∴C1O∥EA,又EA?平面AB1D1;
∴C1O∥平面AB1D1;
(2)如图:补图构成平行六面体ABCD-A1B1C1D1,作B1F⊥A1D1于F,
连AF,∵B1F⊥DD1,DD1∩A1D1=D1,
∴B1F⊥平面ADD1,
∴∠B1AF为直线AB1与平面ADD1所成的角
在△B1AF中可计算出 AB1=
| 2+1 |
| 3 |
| 2 |
| ||
| 2 |

∴在△B1AF中 sin∠B1AF=
| B1F |
| AB1 |
| ||
| 2 |
∴直线AB1与平面ADD1所成的角为
| π |
| 4 |
点评:本题主要考查了线面平行的判定定理及其应用,线面垂直的判定定理及其应用,直线与平面所成的角的作法、证法、算法,将空间问题转化为平面问题的思想方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•河北区一模)已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有
(2012•河北区一模)已知有若干辆汽车通过某一段公路,从中抽取200辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间[60,70)上的汽车大约有 (2012•河北区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=
(2012•河北区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=