题目内容
2.已知f(x)=mx(m为常数,m>0且m≠1).设$f({a_1}),f({a_2}),…,f({a_n})(n∈{N^*})$是首项为4,公比为2的等比数列.(1)求数列{an}的通项公式;
(2)若bn=an•f(an),且数列{bn}的前n项和Sn,当$m=\sqrt{2}$时,求Sn;
(3)若cn=an•f(n),问是否存在实数m,使得数列{cn}中每一项恒小于它后面的项?若存在,求出实数m的取值范围;若不存在,说明理由.
分析 (1)通过求出f(an)的通项公式可知${m^{a_n}}={2^{n+1}}$,并对其两边同时取对数即得结论;
(2)通过(1)可知数列{bn}的通项公式,进而当$m=\sqrt{2}$时利用错位相减法计算即得结论;
(3)通过(1)可知数列{cn}的通项公式,进而只需证明$({n+1}){m^n}{log_m}2<({n+2}){m^{n+1}}{log_m}2$对一切n≥1成立,分m>1、0<m<1两种情况讨论即可.
解答 解:(1)由题意$f({a_n})=4×{2^{n-1}}={2^{n+1}}$,即${m^{a_n}}={2^{n+1}}$,
∴${a_n}={log_m}{2^{n+1}}$…(3分)
(2)由题意${b_n}={a_n}f({a_n})=({{{log}_m}{2^{n+1}}})×{2^{n+1}}=({n+1}){2^{n+1}}{log_m}2$,
当$m=\sqrt{2}$时,${b_n}=({n+1}){2^{n+1}}{log_m}2=({n+1}){2^{n+1}}{log_{\sqrt{2}}}2=({n+1}){2^{n+2}}$.
∴${S_n}=2•{2^3}+3•{2^4}+4•{2^5}+…+(n+1)•{2^{n+2}}$①…(5分)
①式两端同乘以2,得:
$2{S_n}=2•{2^4}+3•{2^5}+4•{2^6}+…+n•{2^{n+2}}+(n+1)•{2^{n+3}}$②
②-①并整理,得:
${S_n}=-2•{2^3}-{2^4}-{2^5}-{2^6}-…-{2^{n+2}}+(n+1)•{2^{n+3}}$
=-23-[23+24+25+…+2n+2]+(n+1)•2n+3
=$-{2^3}-\frac{{{2^3}[1-{2^n}]}}{1-2}+(n+1)•{2^{n+3}}$
=-23+23(1-2n)+(n+1)•2n+3
=n•2n+3…(9分)
(3)结论:当$0<m<\frac{2}{3}$或m>1时,使得数列{cn}中每一项恒小于它后面的项.
理由如下:
由题意${c_n}={a_n}f(n)=({{{log}_m}{2^{n+1}}})×{m^n}=({n+1}){m^n}{log_m}2$,
要使cn<cn+1对一切n≥1成立,
即$({n+1}){m^n}{log_m}2<({n+2}){m^{n+1}}{log_m}2$对一切n≥1成立,
①当m>1时,(n+1)<(n+2)m对一切n≥1成立; …(12分)
②当0<m<1时,(n+1)>(n+2)m,
∴$m<\frac{n+1}{n+2}$一切n≥1成立,
即$m<\frac{2}{3}$,考虑到0<m<1,
∴$0<m<\frac{2}{3}$. …(15分)
综上,当$0<m<\frac{2}{3}$或m>1时,数列{cn}中每一项恒小于它后面的项. …(16分)
点评 本题是一道关于数列的综合题,涉及对数的运算、数列的单调性、数列的通项及前n项和等基础知识,考查错位相减法,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{x^2}{10}-\frac{y^2}{10}$=1 | B. | $\frac{y^2}{10}-\frac{x^2}{10}$=1 | C. | $\frac{x^2}{8}-\frac{y^2}{8}$=1 | D. | $\frac{y^2}{8}-\frac{x^2}{8}=1$ |
| A. | 2,-4 | B. | -2,4 | C. | 2 | D. | -4 |
| A. | (1,$\frac{\sqrt{5}}{2}$] | B. | (1,$\frac{\sqrt{7}}{2}$] | C. | [$\frac{\sqrt{5}}{2}$,+∞) | D. | [$\frac{\sqrt{7}}{2}$,+∞) |
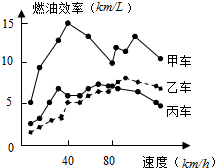 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )