函数y=x-sinx.x∈[$\frac{π}{2}$.π]的最大值是( )A．$\frac{π}{2}-1$B．π-1C．πD．π+1 题目和参考答案——青夏教育精英家教网——

题目内容

18．函数y=x-sinx，x∈[$\frac{π}{2}$，π]的最大值是（　　）

A．

$\frac{π}{2}-1$

B．

π-1

C．

π

D．

π+1

分析先求出函数的导数，得到函数在区间上递增，从而求出函数的最大值．

解答解：y′=1-cosx≥0，
∴函数y=x-sinx在区间[$\frac{π}{2}$，π]递增，
∴y_最大值=π-sinπ=π，
故选：C．

点评本题考查了函数的单调性，函数的最值问题，考查导数的应用，是一道基础题．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

8．已知$cosα=-\frac{4}{5}，sinβ=-\frac{3}{4}，α∈（{\frac{π}{2}，π}），β∈（{π，\frac{3}{2}π}）$，求cos（α-β）

9．某学院为了调查本校学生2014年9月“健康上网”（健康上网是指每天上网不超过两个小时）的天数情况，随机抽取了40名本校学生作为样本，统计他们在该月30天内健康上网的天数，并将所得的数据分成以下六组；[0，5]，（5，10]，（10，15]，…，（25，30]，由此画出样本的频率分布直方图，如图所示，则这40名学生中健康上网天数超过20天的人数10．

6．复数z满足（-1+i）z=（1+i）²，其中i为虚数单位，则在复平面上复数z的共轭复数$\overline z$对应的点位于第一象限．

13．如图的框图表示的算法的功能是（　　）

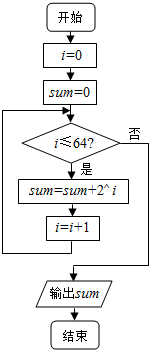
	A．	求和S=2+2²+…+2⁶⁴		B．	求和S=1+2+2²+…+2⁶³
	C．	求和S=1+2+2²+…+2⁶⁴		D．	以上均不对

3．从1，2，3，4，5，6中选出3个不同的数组成3位数，并将这些三位数由小到大打排列，则第100个数是564．

10．命题“?x₀∈R，2${\;}^{{x}_{0}}$≥1”的否定是（　　）

?x₀∈R，2${\;}^{{x}_{0}}$＜1

?x₀∈R，2${\;}^{{x}_{0}}$≤1

?x∈R，2^x≥1

?x∈R，^x＜1

7．化简：$\frac{cos（π+α）ta{n}^{2}（2π-α）cos（α-3π）}{sin（π-α）sin（2π-α）}$．

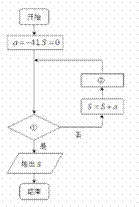右图表示的是求首项为-41，公差为2的等差数列{a_n}前n项和的最小值的程序框图．①处可填写a＞0；②处可填写a=a+2．