题目内容
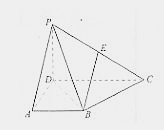
【题目】在四棱锥P—ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)求证:BC⊥平面PBD;
(Ⅲ)设Q为侧棱PC上一点,![]() 试确定
试确定![]() 的值,使得二面角Q—BD—P为45°.
的值,使得二面角Q—BD—P为45°.
【答案】(Ⅰ)略
(Ⅱ)略
(Ⅲ)![]()
【解析】
解:(1)取PD的中点F,连接EF,AF,
因为E为PC中点,所以EF//CD,且![]() ,
,
在梯形ABCD中,AB//CD,AB=1,
所以EF//AB,EF=AB,四边形ABEF为平行四边形,
所以BE//AF,
BE![]() 平面PAD,AF
平面PAD,AF![]() 平面PAD,
平面PAD,
所以BE//平面PAD.
(2)平面PCD⊥底面ABCD,PD⊥CD,

所以PD⊥平面ABCD,
所以PD⊥AD.
如图,以D为原点建立空间直角坐标系Dxyz.
则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1)
![]()
所以![]()
又由PD⊥平面ABCD,可得PD⊥BC,
所以BC⊥平面PBD.

(3)平面PBD的法向量为![]() =(-1,1,0)
=(-1,1,0)
![]()
所以Q![]()
设平面QBD的法向量为![]()
则![]() ,
,
所以![]() ,
,
所以
注意到![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目