题目内容
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
【答案】(I)首先设椭圆的半焦距为![]() ,根据题意得到
,根据题意得到![]() ,结合椭圆中
,结合椭圆中![]() 的关系,得到
的关系,得到![]() ,化简得出
,化简得出![]() ,从而求得其离心率;
,从而求得其离心率;
(II)结合(I)的结论,设出椭圆的方程![]() ,写出直线的方程,两个方程联立,求得交点的坐标,利用直线与圆相切的条件,列出等量关系式,求得
,写出直线的方程,两个方程联立,求得交点的坐标,利用直线与圆相切的条件,列出等量关系式,求得![]() ,从而得到椭圆的方程.
,从而得到椭圆的方程.
【解析】
(I)![]() ;
;
(II)![]() .
.
(I)解:设椭圆的半焦距为![]() ,由已知有
,由已知有![]() ,
,
又由![]() ,消去
,消去![]() 得
得![]() ,解得
,解得![]() ,
,
所以,椭圆的离心率为![]() .
.
(II)解:由(I)知,![]() ,故椭圆方程为
,故椭圆方程为![]() ,
,
由题意,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标满足
的坐标满足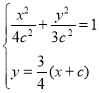 ,消去
,消去![]() 并化简,得到
并化简,得到![]() ,
,
解得![]() ,
,
代入到![]() 的方程,解得
的方程,解得![]() ,
,
因为点![]() 在
在![]() 轴的上方,所以
轴的上方,所以![]() ,
,
由圆心在直线![]() 上,可设
上,可设![]() ,因为
,因为![]() ,
,
且由(I)知![]() ,故
,故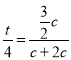 ,解得
,解得![]() ,
,
因为圆![]() 与
与![]() 轴相切,所以圆的半径为2,
轴相切,所以圆的半径为2,
又由圆![]() 与
与![]() 相切,得
相切,得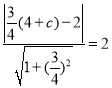 ,解得
,解得![]() ,
,
所以椭圆的方程为:![]() .
.

练习册系列答案
相关题目
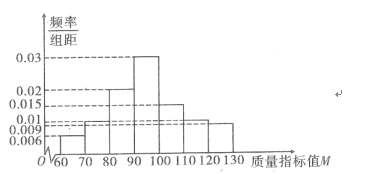
【题目】某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.
(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01)