题目内容
【题目】设p：f（x）＝1+ax,在（0，2]上f（x）≥0恒成立,q函数g（x）＝ax+2lnx在其定义域上存在极值．
(1)若p为真命题,求实数a的取值范围；
(2)如果“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围．
【答案】(1)[
，+∞）(2)（﹣∞，）∪[0，+∞）
【解析】
(1)进行常变量分离,求出反比例函数在区间（0，2]的取值范围,最后可以求出实数a的取值范围；
(2)求出当q为真命题时, 实数a的取值范围,然后根据或命题的真假的定义,分类讨论求出实数a的取值范围．
(1)若p为真命题，则a
，x∈（0，2]恒成立，所以a≥（
）max，当x∈（0，2]时
,即a的取值范围为[，+∞）；
(2)若q为真命题：函数g（x）＝ax+2lnx在其定义域上存在极值；
由于g′（x）＝a
,x＞0
若a≥0,g'（x）＞0，g（x）在定义域单调递增，在其定义域上不存在极值，不符合题意；
若a＜0,则g′（x）＝a
0，则x
，
当0＜x
时,g'（x）＞0，g（x）单调递增；
当x
时,g'（x）＜0，g（x）单调递减；
∴x时,g（x）在x时有极大值
所以，若q为真命题，则a＜0.
因为“p或q”为真命题,“p且q”为假命题,所以命题p与q一真一假.
①p真q假时,则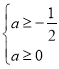
，解得a≥0，
②p假q真时,则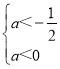
，解得a
；
综上所述:a的取值范围为（﹣∞，）∪[0，+∞）．
练习册系列答案
相关题目
