题目内容
给出下列命题:①a>b⇒ac2>bc2; ②a>|b|⇒a2>b2; ③a>b⇒a3>b3;
④|a|>b⇒a2>b2.其中正确的命题是( ).
| A.①② | B.②③ | C.③④ | D.①④ |
B
解析试题分析:当c=0时,a>b⇒ac2>bc2不成立,故①为假命题;
若a>|b|成立,则a>|b|≥0,此时a2>b2一定成立,故②为真命题;
当a>b时,三次幂函数的单调性可得,a3>b3一定成立,故③为真命题;
当a=b=-1时,|a|>b成立,但a2>b2不成立,故④为假命题。故选B。
考点:本题主要考查不等式的性质。
点评:简单题,涉及命题真假判断问题,一半要逐一考察各个命题,作出结论。

练习册系列答案
相关题目
命题“对任意的 ”的否定是
”的否定是
A.不存在 | B.存在 |
C.存在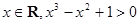 | D.对任意的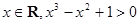 |
非零向量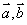 使得
使得 成立的一个充分非必要条件是
成立的一个充分非必要条件是
A. | B. |
C. | D. |
已知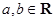 ,下列四个条件中,使“
,下列四个条件中,使“ ”成立的必要而不充分的条件是( )
”成立的必要而不充分的条件是( )
A. | B. | C. | D. |
命题 对
对 ,都有
,都有 成立,则
成立,则 的否定形式为( )
的否定形式为( )
A.对 ,都有 ,都有 | B. ,都有 ,都有 |
C. ,都有 ,都有 | D.对 ,都有 ,都有 |
“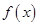 在[a,b]上为单调函数”是“函数
在[a,b]上为单调函数”是“函数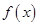 在[a,b]上有最大值和最小值”的( )
在[a,b]上有最大值和最小值”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也非必要条件 |
对于函数 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )
A. | B. |
C. | D. |
设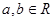 ,
, 是虚数单位,则“
是虚数单位,则“ ”是“复数
”是“复数 为纯虚数”的 ( )
为纯虚数”的 ( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 ,则
,则 是
是
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |