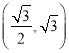Question

【题目】已知向量 =（ sin3x，﹣y）， =（m，cos3x﹣m）（m∈R），且 + = ．设y=f（x）．
（1）求f（x）的表达式，并求函数f（x）在[ ， ]上图象最低点M的坐标．
（2）在△ABC中，f（A）=﹣ ，且A＞ π，D为边BC上一点，AC= DC，BD=2DC，且AD=2 ，求线段DC的长．

Answer 1

【答案】
（1）解：向量 =（ sin3x，﹣y）， =（m，cos3x﹣m）（m∈R），

∴ + =（m+ sin3x，﹣y+cos3x﹣m），

∵ + = ．

m+ sin3x=0，﹣y+cos3x﹣m=0

∴y=cos3x+ sin3x

即y=f（x）=2sin（3x+ ）

∴f（x）的表达式f（x）=2sin（3x+ ）

∵x在[ ， ]上，

∴3x+ ∈[ ， ]，

当3x+ = 时，取得最低点，此时x= ，y=﹣1．

∴函数f（x）在[ ， ]上图象最低点M的坐标为（ ，﹣1）．

（2）解：由f（A）=﹣ ，即2sin（3A+ ）=

可得：3A+ = +2kπ或3A+ = +2kπ，k∈Z．

∵π＞A＞ π，

∴A= ．

∴△ABC是直角三角形．

AC= DC，BD=2DC，

设DC=x，则AC= x，BD=2x，BC=3x．

可得：AB= ．

在三角形ADB和三角形ADC中，由余弦定理：可得cos∠BDA=

cos∠ADC= ，

∵∠ADC+∠BDA=π．

∴ =﹣ ，

解得：x= ．

∴线段DC的长为 ．

【解析】（1）根据 + = ．用x表示y可得f（x）的表达式．即可求函数f（x）在[ ， ]上图象最低点M的坐标．（2）根据f（A）=﹣ ，且A＞ π，求出A，AC= DC，BD=2DC，且AD=2 ，利用余弦定理求出线段DC的长．