题目内容
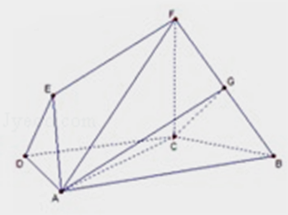
【题目】如图,在梯形ABCD中,AB∥C,AD=DC=CB=1,∠ABC═60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1. 
(1)求证:BC⊥平面ACFE;
(2)求二面角A﹣BF﹣C的平面角的余弦值;
(3)若点M在线段EF上运动,设平MAB与平FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
【答案】
(1)证明:在梯形ABCD中,∵AB∥CD,AD=DC=CB=1,∠ABC=60°,
∴AB=2,AC2=AB2+BC2﹣2ABBCcos60°=3,
∴AB2=AC2+BC2,∴BC⊥AC,
∵平面ACFE⊥平面ABCD,
平面ACFE∩平面ABCD=AC,BC平面ABCD,
∴BC⊥平面ACFE.
(2)解:取FB中点G,连接AG,CG,
∵AF= ![]() =2,∴AB=AF,∴AG⊥FB,
=2,∴AB=AF,∴AG⊥FB,
∵CF=CB=1,∴CG⊥FB,∴∠AGC=θ,
∵BC=CF,∴FB= ![]() ,∴CG=
,∴CG= ![]() ,AG=
,AG= ![]() ,
,
∴cosθ= ![]() =
= ![]() .
.
(3)解:由(2)知:
①当M与F重合时,cosθ= ![]() .
.
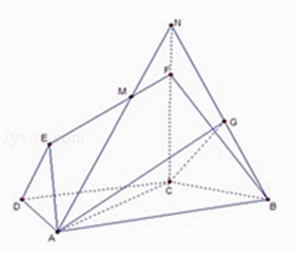
②当M与E重合时,过B作BN∥CF,且使BN=CF,
连接EN,FN,则平面MAB∩平面FCB,
∵BC⊥CF,AC⊥CF,∴CF⊥平面ABC,∴BN⊥平面ABC,
∴∠ABC=θ,∴θ=60°,∴cosθ= ![]() .
.
③当M与E,F都不重合时,令FM=λ,0<λ< ![]() ,
,
延长AM交CF的延长线于N,连接BN,
∴N在平面MAB与平面FCB的交线上,
∵B在平面MAB与平面FCB的交线上,
∴平面MAB∩平面FCB=BN,
过C作CH⊥NB交NB于H,连接AH,
由(1)知,AC⊥BC,
又∵AC⊥CN,∴AC⊥平面NCB,∴AC⊥NB,
又∵CH⊥NB,AC∩CH=C,∴NB⊥平面ACH,
∴AH⊥NB,∴∠AHC=θ,
在△NAC中,NC= ![]() ,
,
从而在△NCB中,CH= ![]() ,
,
∵∠ACH=90°,∴AH= ![]() =
= ![]() ,
,
∴cosθ= ![]() =
= ![]() ,
,
∵0 ![]() ,
,
∴ ![]() ,
,
综上所述,cosθ∈[ ![]() ,
, ![]() ].
].
【解析】(1)在梯形ABCD中,由AB∥CD,AD=DC=CB=1,∠ABC=60°,推导出AB2=AC2+BC2 , BC⊥AC,由平面ACFE⊥平面ABCD,能证明BC⊥平面ACFE.(2)取FB中点G,连接AG,CG,由AF= ![]() =2,知AB=AF,AG⊥FB,由CF=CB=1,CG⊥FB,∠AGC=θ,由此能求出二面角A﹣BF﹣C的平面角的余弦值.(3)由点M在线段EF上运动,分当M与F重合,M与E重合时,当M与E,F都不重合三种情况进行分类讨论,能求出cosθ的取值范围.
=2,知AB=AF,AG⊥FB,由CF=CB=1,CG⊥FB,∠AGC=θ,由此能求出二面角A﹣BF﹣C的平面角的余弦值.(3)由点M在线段EF上运动,分当M与F重合,M与E重合时,当M与E,F都不重合三种情况进行分类讨论,能求出cosθ的取值范围.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 考前必练系列答案
考前必练系列答案