题目内容
10.已知数列{an}满足:a1+2a2+…+nan=2-$\frac{n+2}{2^n}$(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2$\frac{1}{2a_n^2},且{c_n}=\frac{b_n}{a_n}$,求数列{cn}的前n项和Tn.
分析 (I)利用递推关系即可得出;
(II)bn=log2$\frac{1}{2{a}_{n}^{2}}$=2n-1,${c}_{n}=\frac{{b}_{n}}{{a}_{n}}$=(2n-1)•2n,利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(I)∵a1+2a2+…+nan=2-$\frac{n+2}{2^n}$,
∴当n=1时,a1=$\frac{1}{2}$.
当n≥2时,a1+2a2+…+(n-1)an-1=2-$\frac{n+1}{{2}^{n-1}}$,可得nan=$\frac{n}{{2}^{n}}$,即an=$\frac{1}{{2}^{n}}$.
当n=1时也满足上式,
∴an=$\frac{1}{{2}^{n}}$.
(II)bn=log2$\frac{1}{2{a}_{n}^{2}}$=2n-1,${c}_{n}=\frac{{b}_{n}}{{a}_{n}}$=(2n-1)•2n.
∴数列{cn}的前n项和Tn=2+3×22+5×23+…+(2n-1)•2n.
∴$2{T}_{n}={2}^{2}+3×{2}^{3}$+…+(2n-3)•2n+(2n-1)•2n+1.
∴-Tn=2+2×22+…+2×2n-(2n-1)•2n+1=$\frac{4({2}^{n}-1)}{2-1}$-2-(2n-1)•2n+1=(3-2n)•2n+1-6.
∴Tn=(2n-3)•2n+1+6.
点评 本题考查了“错位相减法”与等比数列的前n项和公式、递推关系的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1.下列能表示函数图象的是( )
| A. | 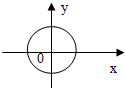 | B. | 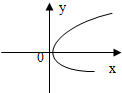 | C. |  | D. | 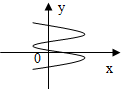 |
5.已知log${\;}_{\frac{1}{2}}$a<log${\;}_{\frac{1}{2}}$b,则下列不等式一定成立的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | ${({\frac{1}{3}})^a}>{({\frac{1}{3}})^b}$ | C. | ln(a-b)>0 | D. | 3a-b>1 |
15.对于任意实数x,符号[x]表示不超过x的最大整数(如[-1.5]=-2,[0]=0,[2.3]=2),则[log2$\frac{1}{4}$]+[log2$\frac{1}{3}$]+[log21]+[log23]+[log24]的值为( )
| A. | 0 | B. | -2 | C. | -1 | D. | 1 |
1.在极坐标系中,曲线$ρ=4sin(θ-\frac{π}{3})$关于( )
| A. | 直线θ=$\frac{π}{3}$对称 | B. | 直线θ=$\frac{5π}{6}$对称 | C. | 点$(2,\frac{π}{3})$对称 | D. | 极点对称 |