题目内容
【题目】已知椭圆 
=1（a＞b＞0）经过点P（﹣2，0）与点（1，1）．
（1）求椭圆的方程；
（2）过P点作两条互相垂直的直线PA，PB，交椭圆于A，B．
①证明直线AB经过定点；
②求△ABP面积的最大值．
【答案】
（1）解：由题意可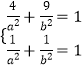得 
，解得 
，
∴椭圆方程为 
（2）①证明：由对称性知，若存在定点，则必在x轴上，
当kPA=1时，lPA：y=x+2，
联立 
，得x2+3x+2=0，解得x=﹣1．
下面验证定点为（1，0）．
设直线PA的方程为y=k（x+2），
联立 ，得（1+3k2）x2+12k2x+12k2﹣4=0，
解得： 
．
同理可得： 
．
则 
，即直线AB经过定点（﹣1，0）；
②解：由题意可知，直线不与x轴平行，设直线AB方程为x=ty﹣1．
联立 
，得（t2+3）y2﹣2ty﹣3=0．
∴ 
，
∴ 
= 
．
令 
，λ∈[3，+∞），则 
．
∴ 
．
当且仅当λ=3，即t=0时成立
【解析】（1）把已知点的坐标代入椭圆方程，求解方程组可得a，b，则椭圆的方程可求；（2）①由对称性知，若存在定点，则必在x轴上，求出PA所在直线斜率为1时AB所过定点，验证得答案；②设直线AB方程为x=ty﹣1．联立直线方程和椭圆方程，化为关于y的一元二次方程，利用根与系数的关系求得A，B的纵坐标的和与积，结合弦长公式求得面积，换元后利用基本不等式求最值．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
阅读快车系列答案
相关题目
