题目内容
【题目】已知边长为![]() 的正方形
的正方形![]() 与菱形
与菱形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() 为
为![]() 中点.
中点.
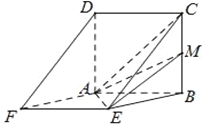
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求四面体
,求四面体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)证明BC∥AD.说明BC∥平面ADF.通过证明平面BCE∥平面ADF.推出EM∥平面ADF.
(Ⅱ)取AB中点P,连结PE.证明EP⊥平面ABCD,然后利用等体积法求解即可.
试题解析:
(1)∵四边形ABCD是正方形,∴BC∥AD.∵BC![]() 平面ADF,AD平面ADF,
平面ADF,AD平面ADF,
∴BC∥平面ADF.∵四边形ABEF是菱形,
∴BE∥AF.
∵BE![]() 平面ADF,AF平面ADF,
平面ADF,AF平面ADF,
∴BE∥平面ADF.∵BC∥平面ADF,BE∥平面ADF,BC∩BE=B,
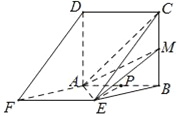
∴平面BCE∥平面ADF.
∵EM平面BCE,∴EM∥平面ADF.
(2)取AB中点P,连结PE.∵在菱形ABEF中,∠ABE=60°,
∴△AEB为正三角形,∴EP⊥AB.∵AB=2,∴EP=![]() .
.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
∴EP⊥平面ABCD, ∴EP为四面体E﹣ACM的高.
∴![]()

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目


