题目内容
【题目】“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因.暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数.当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,0.2≤x≤2时,排水量V是垃圾杂物密度x的一次函数.
(1)当0≤x≤2时,求函数V(x)的表达式;
(2)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时)f(x)=xV(x)可以达到最大,求出这个最大值.
【答案】
(1)解:∵当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时,
∴V(x)=90,0≤x≤0.2,
∵0.2≤x≤2时,排水量V是垃圾杂物密度x的一次函数,
∴设为V(x)=mx+n,将(0.2,90),(2,0)代入得:
![]() ,解得m=﹣50,n=100,
,解得m=﹣50,n=100,
∴V(x)=﹣50x+100,0.2≤x≤2,
∴ ![]()
(2)解:由题意可得 ![]() ,
,
当0≤x≤0.2时,f(x)=90x,最大值为1.8千克/小时,
当0.2≤x≤2时,f(x)=50x(2﹣x)≤50(x=1时取等号),
∴当杂物垃圾密度x=1千克/立方米,f(x)取得最大值50千克/小时
【解析】(1)根据题意,对x进行分段求解,当0≤x≤0.2,V(x)=90,当0.2≤x≤2时,利用待定系数法,求出V(x)=﹣50x+100,最后用分段函数表示出V(x)即可;(2)表示出f(x)的解析式为分段函数,对0≤x≤0.2上的函数利用单调性求最大值,对0.2≤x≤2上的函数运用基本不等式求最大值,比较两段的最大值,即可得到答案.

【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入,已知研发投入![]() (十万元)与利润
(十万元)与利润![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由资料知![]() 对
对![]() 呈线性相关关系。试求:
呈线性相关关系。试求:
(1)线性回归方程![]() ;
;
(2)估计![]() 时,利润是多少?
时,利润是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式:
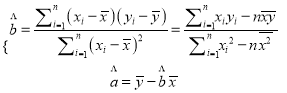
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.