题目内容
已知A、B、C三点在球心为O,半径为3的球面上,且几何体O-ABC为正三棱锥,若A、B两点的球面距离为π,则正三棱锥的侧面与底面所成角的余弦值为______.
作出图形,
∵A、B两点的球面距离为π,
∴球心角∠AOB=
,
∵OA=OB=3,∴AB=3.
∵几何体O-ABC为正三棱锥,∴几何体O-ABC为正四面体,
设正四面体O-ABC的棱长为2,取AC中点D,连接OD,BD,
∵OA=OC=AC=AB=BC=2,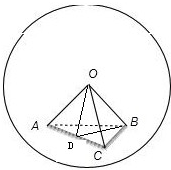
∴OD⊥AC,BD⊥AC,OD=BD=
,
∴∠ODB是正三棱锥的侧面与底面所成角,
∴cos∠ODB=
=
.
故答案为:
.
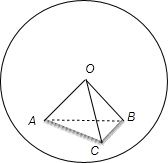
∵A、B两点的球面距离为π,
∴球心角∠AOB=
| π |
| 3 |
∵OA=OB=3,∴AB=3.
∵几何体O-ABC为正三棱锥,∴几何体O-ABC为正四面体,
设正四面体O-ABC的棱长为2,取AC中点D,连接OD,BD,
∵OA=OC=AC=AB=BC=2,

∴OD⊥AC,BD⊥AC,OD=BD=
| 3 |
∴∠ODB是正三棱锥的侧面与底面所成角,
∴cos∠ODB=
(
| ||||
2×
|
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目