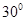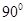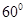题目内容
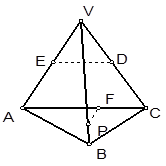
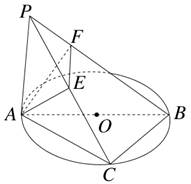
如图,PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上的一点,E、F分别是点A在PB、PC上的射影.给出下列结论:
①AF⊥PB; ②EF⊥PB;
③AF⊥BC; ④AE⊥平面PBC.
其中正确命题的序号是 .

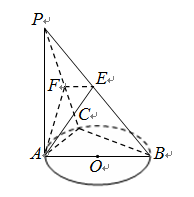
①AF⊥PB; ②EF⊥PB;
③AF⊥BC; ④AE⊥平面PBC.
其中正确命题的序号是 .
①②③
试题分析:
 所在的平面
所在的平面 ,
,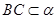 ,
,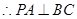 ,又
,又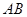 为圆
为圆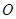 的直径,
的直径,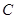 是圆
是圆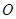 上的一点,
上的一点,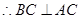 ,又
,又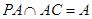 ,
, 平面
平面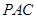 ,
,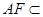 平面
平面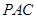 ,
,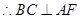 ,又
,又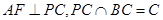 ,
,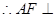 平面
平面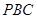 ,又
,又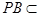 平面
平面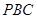 ,
,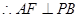 ,即①正确;
,即①正确;又
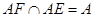 ,故
,故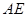 不与平面
不与平面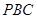 垂直,即④错误;
垂直,即④错误;又
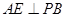 ,同理可证
,同理可证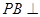 平面
平面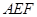 ,
,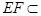 平面
平面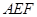 ,
,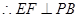 ,即②正确;
,即②正确;由
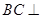 平面
平面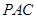 ,
,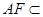 平面
平面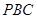 知,
知,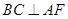 ,即③正确;
,即③正确;故答案为①②③.

练习册系列答案
相关题目
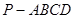 的底面为菱形,
的底面为菱形,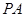
 面
面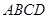 ,且
,且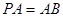 ,
,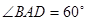 ,
,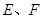 分别是
分别是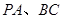 的中点.
的中点.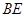 ∥平面
∥平面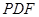 ;
;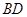 作一平面交棱
作一平面交棱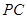 于点
于点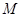 ,若二面角
,若二面角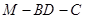 的大小为
的大小为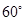 ,求
,求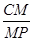 的值.
的值.
 中,
中,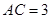 ,
,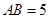 ,
,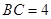 ,
,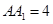 ,点
,点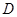 是
是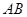 的中点.
的中点.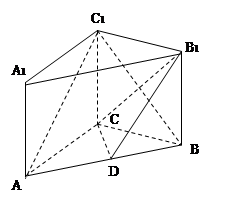
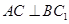 ;
; 
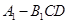 的体积.
的体积.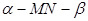 的大小为
的大小为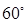 ,菱形
,菱形 在面
在面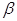 内,
内,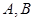 两点在棱
两点在棱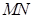 上,
上,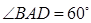 ,
,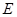 是
是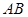 的中点,
的中点,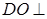 面
面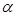 ,垂足为
,垂足为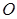 .
.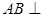 平面
平面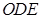 ;
;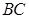 与
与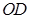 所成角的余弦值.
所成角的余弦值.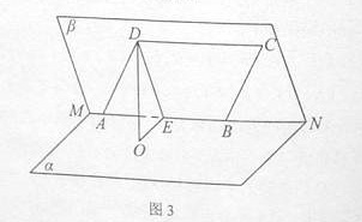
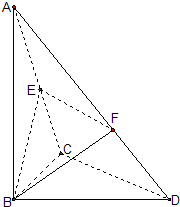
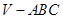 中,
中,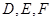 分别是
分别是 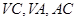 的中点,
的中点,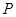 为
为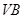 上任意一点,则直线
上任意一点,则直线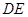 与
与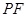 所成的角的大小是 ( )
所成的角的大小是 ( )