题目内容
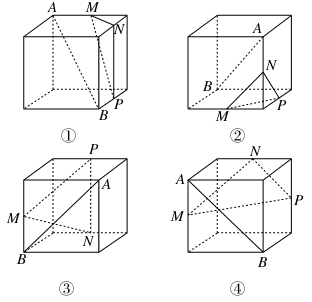
如图,正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F.求证:EF∥平面ABCD.
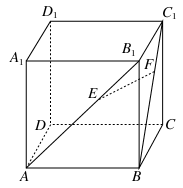

见解析
证明:方法一:过E作EM⊥AB于M,过F作FN⊥BC于N,连接MN,如图所示,则EM∥BB1,FN∥BB1,
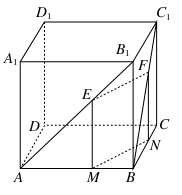
∴EM∥FN.
∵AB1=BC1,B1E=C1F,
∴AE=BF,
∴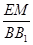 =
=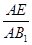 ,
,
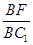 =
=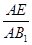 =
=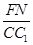 ,
,
∴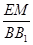 =
=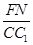 .
.
又∵BB1=CC1,∴EM=FN,
∴四边形EMNF是平行四边形,
∴EF∥MN.
又∵EF?平面ABCD,MN?平面ABCD,
∴EF∥平面ABCD.
方法二:过点E作EH⊥BB1于点H,连接FH,如图所示,则EH∥AB,所以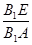 =
=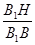 .
.
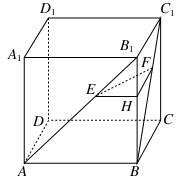
∵AB1=BC1,B1E=C1F,
∴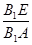 =
=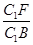 ,
,
∴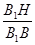 =
=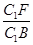 ,
,
∴FH∥B1C1.
∵B1C1∥BC,∴FH∥BC.
∵EH∩FH=H,
∴平面EFH∥平面ABCD.
∵EF?平面EFH,
∴EF∥平面ABCD.

∴EM∥FN.
∵AB1=BC1,B1E=C1F,
∴AE=BF,
∴
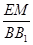 =
=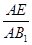 ,
,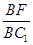 =
=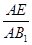 =
=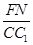 ,
,∴
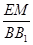 =
=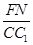 .
.又∵BB1=CC1,∴EM=FN,
∴四边形EMNF是平行四边形,
∴EF∥MN.
又∵EF?平面ABCD,MN?平面ABCD,
∴EF∥平面ABCD.
方法二:过点E作EH⊥BB1于点H,连接FH,如图所示,则EH∥AB,所以
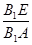 =
=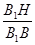 .
.
∵AB1=BC1,B1E=C1F,
∴
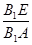 =
=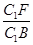 ,
,∴
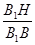 =
=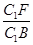 ,
,∴FH∥B1C1.
∵B1C1∥BC,∴FH∥BC.
∵EH∩FH=H,
∴平面EFH∥平面ABCD.
∵EF?平面EFH,
∴EF∥平面ABCD.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
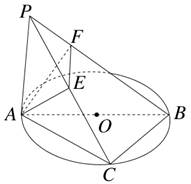
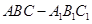 中,
中,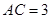 ,
,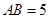 ,
,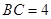 ,
,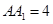 ,点
,点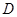 是
是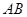 的中点.
的中点.
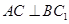 ;
; 
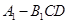 的体积.
的体积.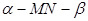 的大小为
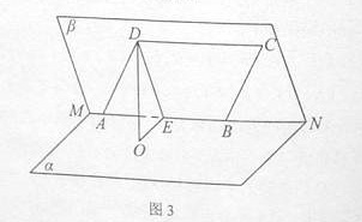
的大小为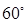 ,菱形
,菱形 在面
在面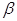 内,
内,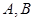 两点在棱
两点在棱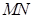 上,
上,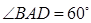 ,
,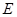 是
是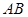 的中点,
的中点,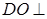 面
面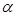 ,垂足为
,垂足为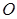 .
.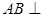 平面
平面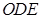 ;
;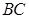 与
与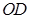 所成角的余弦值.
所成角的余弦值.