题目内容
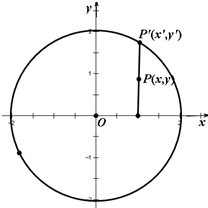
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半(横坐标不变),得到点P,并设点P的轨迹为曲线C.
(1)求C的方程;
(2)设o为坐标原点,过点Q(
,0)的直线l与曲线C交于两点A,B,线段AB的中点为N,且
=2
,点E在曲线C上,求直线l:
+
=1的方程.
(1)求C的方程;
(2)设o为坐标原点,过点Q(
| 3 |
| OE |
| ON |
| x |
| a |
| y |
| b |

(1)设点P(x,y),点P′(x′,y′),由题意可知
,…(2分)
又∵x′2+y′2=4,…(3分)
∴x2+4y2=4⇒
+y2=1.…(5分)
∴点M的轨迹C的方程为
+y2=1.…(6分)
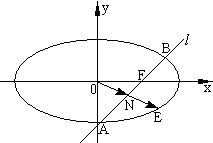
(2)设点A(x1,y1),B(x2,y2),
点N的坐标为(x0,y0),
①当直线l与x轴重合时,线段AB的中点N就是原点O,不合题意,舍去;…(7分)
②设直线l:x=my+
,
由
,消去x,得(m2+4)y2+2
my-1=0…(8分)
∴y0=
=-
,…(9分)
∴x0=my0+
=-
+
=
,…(10分)
∴点N的坐标为(
,-
).…(11分)
由
=2
,则点E的为(
,-
),…(12分)
由点E在曲线C上,
得
+
=1,
即m4-4m2-32=0,∴m2=8(m2=-4舍去).…(13分)
∴直线l的方程为x±2
y-
=0…(14分)
|
又∵x′2+y′2=4,…(3分)
∴x2+4y2=4⇒
| x2 |
| 4 |
∴点M的轨迹C的方程为
| x2 |
| 4 |
(2)设点A(x1,y1),B(x2,y2),
点N的坐标为(x0,y0),
①当直线l与x轴重合时,线段AB的中点N就是原点O,不合题意,舍去;…(7分)
②设直线l:x=my+
| 3 |
由
|
| 3 |
∴y0=
| y1+y2 |
| 2 |
| ||
| m2+4 |
∴x0=my0+
| 3 |
| ||
| m2+4 |
| ||||
| m2+4 |
4
| ||
| m2+4 |
∴点N的坐标为(
4
| ||
| m2+4 |
| ||
| m2+4 |
由
| OE |
| ON |
8
| ||
| m2+4 |
2
| ||
| m2+4 |
由点E在曲线C上,
得
| 48 |
| (m2+4)2 |
| 12m2 |
| (m2+4)2 |
即m4-4m2-32=0,∴m2=8(m2=-4舍去).…(13分)
∴直线l的方程为x±2
| 2 |
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目