题目内容
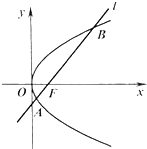
已知曲线C上的动点P到点(1,0)的距离与到定直线L:x=-1的距离相等,
(1)求曲线C的方程;
(2)直线m过(-2,1),斜率为k,k为何值时,直线m与曲线C只有一个公共点,有两个公共点;没有公共点?
(1)求曲线C的方程;
(2)直线m过(-2,1),斜率为k,k为何值时,直线m与曲线C只有一个公共点,有两个公共点;没有公共点?
(1)由抛物线的定义可知动点P的轨迹是抛物线:y2=4x.
(2)设直线m的方程为y-1=k(x+2),联立
.
化为k2x2+(4k2+2k-4)x+4k2+4k+1=0.
①当k=0时,直线m∥x轴,直线与抛物线只有一个交点,满足题意;
②当k≠0时,若直线与m相切时,直线m与抛物线有且只有一个公共点,此时△=0,化为2k2+k-1=0,解得k=-1或k=
.
当直线m与抛物线相交时,线m与抛物线有两个公共点,此时△>0,化为2k2+k-1<0,解得-1<k<
.(k≠0).
当△<0,直线m与抛物线没有公共点,由△<0化为2k2+k-1>0,解得k>
或k<-1.
综上可知:当k=0或k=-1或k=
时,直线与抛物线只有一个公共点;
当-1<k<
且k≠0时,直线与抛物线有两个公共点;
当k>
或k<-1时,直线m与抛物线没有公共点.
(2)设直线m的方程为y-1=k(x+2),联立
|
化为k2x2+(4k2+2k-4)x+4k2+4k+1=0.
①当k=0时,直线m∥x轴,直线与抛物线只有一个交点,满足题意;
②当k≠0时,若直线与m相切时,直线m与抛物线有且只有一个公共点,此时△=0,化为2k2+k-1=0,解得k=-1或k=
| 1 |
| 2 |
当直线m与抛物线相交时,线m与抛物线有两个公共点,此时△>0,化为2k2+k-1<0,解得-1<k<
| 1 |
| 2 |
当△<0,直线m与抛物线没有公共点,由△<0化为2k2+k-1>0,解得k>
| 1 |
| 2 |
综上可知:当k=0或k=-1或k=
| 1 |
| 2 |
当-1<k<
| 1 |
| 2 |
当k>
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目