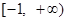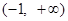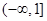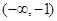题目内容
已知函数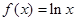 ,
, 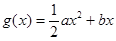
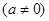 .
.
(1)若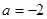 , 函数
, 函数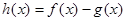 在其定义域是增函数,求
在其定义域是增函数,求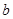 的取值范围;
的取值范围;
(2)在(1)的结论下,设函数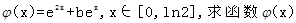 的最小值;
的最小值;
(3)设函数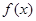 的图象
的图象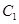 与函数
与函数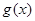 的图象
的图象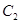 交于点
交于点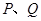 ,过线段
,过线段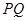 的中点
的中点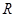 作
作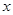 轴的垂线分别交
轴的垂线分别交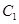 、
、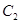 于点
于点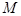 、
、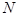 ,问是否存在点
,问是否存在点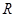 ,使
,使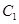 在
在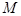 处的切线与
处的切线与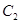 在
在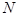 处的切线平行?若存在,求出
处的切线平行?若存在,求出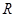 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
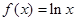 ,
, 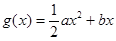
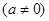 .
.(1)若
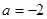 , 函数
, 函数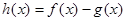 在其定义域是增函数,求
在其定义域是增函数,求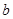 的取值范围;
的取值范围;(2)在(1)的结论下,设函数
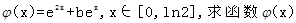 的最小值;
的最小值;(3)设函数
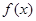 的图象
的图象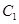 与函数
与函数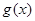 的图象
的图象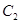 交于点
交于点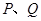 ,过线段
,过线段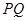 的中点
的中点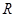 作
作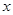 轴的垂线分别交
轴的垂线分别交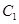 、
、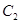 于点
于点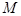 、
、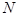 ,问是否存在点
,问是否存在点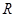 ,使
,使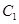 在
在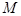 处的切线与
处的切线与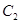 在
在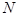 处的切线平行?若存在,求出
处的切线平行?若存在,求出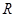 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.(1)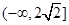 ;(2)当
;(2)当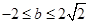 时,
时,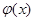 的最小值为
的最小值为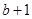 ;当
;当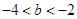 时,
时,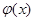 的最小值为
的最小值为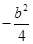 ;当
;当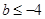 时,
时,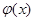 的最小值为
的最小值为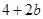 ;(3)不存在点.
;(3)不存在点.
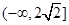 ;(2)当
;(2)当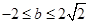 时,
时,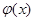 的最小值为
的最小值为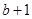 ;当
;当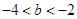 时,
时,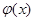 的最小值为
的最小值为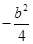 ;当
;当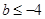 时,
时,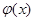 的最小值为
的最小值为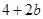 ;(3)不存在点.
;(3)不存在点.试题分析:本题主要考查导数的运算,利用导数研究函数的单调性、不等式基础知识,考查函数思想、构造函数思想、分类讨论思想,考查综合分析和解决问题的能力.第一问,利用导数研究函数的单调性,转化为恒成立问题,再转化为求函数最值问题;第二问,利用配方法求最值,讨论对称轴与区间端点的大小,本问突出体现了分类讨论思想的运用;第三问,把问题坐标化,用反证法证明,利用切线平行,列出方程,构造函数,判断单调性求最值,得出矛盾.
试题解析:(1)依题意:
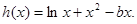
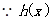 在
在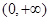 上是增函数,
上是增函数,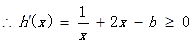 对
对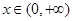 恒成立, 2分
恒成立, 2分∴
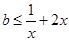
∵
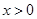 ,则
,则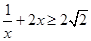 .
.∴
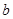 的取值范围为
的取值范围为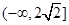 4分
4分(2)设
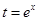 ,则函数化为
,则函数化为
∵
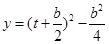
∴当
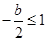 ,即
,即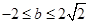 时,函数
时,函数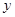 在
在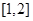 上为增函数.
上为增函数.当
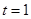 时,
时,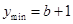 ; 6分
; 6分当
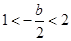 ,即
,即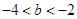 时,当
时,当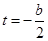 时,
时,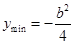 ;
;当
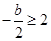 ,即
,即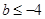 时,函数
时,函数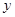 在
在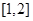 上是减函数.
上是减函数.当
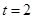 时,
时,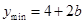 8分
8分综上所述,当
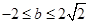 时,
时,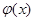 的最小值为
的最小值为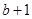 .
.当
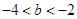 时,
时,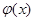 的最小值为
的最小值为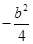 .
.当
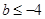 时,
时,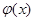 的最小值为
的最小值为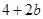 . 9分
. 9分(3)设点
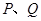 的坐标是
的坐标是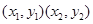 且
且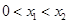 则点
则点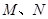 的横坐标为
的横坐标为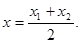
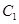 在点
在点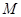 处的切线斜率为
处的切线斜率为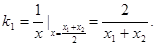
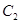 在点
在点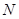 处的切线斜率为
处的切线斜率为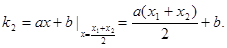 10分
10分假设
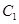 在点
在点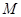 处的切线与
处的切线与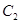 在点
在点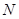 处的切线平行,则
处的切线平行,则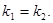
则
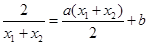 11分
11分则
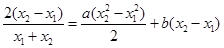
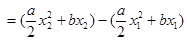
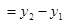
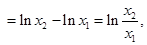
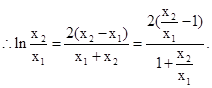
设
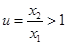 ,则
,则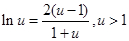 ① 12分
① 12分令
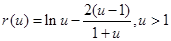 ,则
,则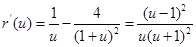
∵
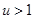 ,∴
,∴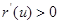 ,所以
,所以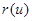 在
在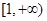 上单调递增,
上单调递增,故
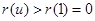 ,则
,则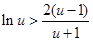 .
.这与①矛盾,假设不成立.故C1在点M处的切线与C2在点N处的切线不平行. 14分

练习册系列答案
相关题目
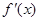 >
>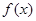 成立,则称函数
成立,则称函数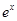 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围;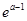 g(1)的大小;
g(1)的大小;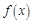 是偶函数,且当
是偶函数,且当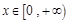 时,f (x) = x-1,则f (x-1) < 0的解集是( )
时,f (x) = x-1,则f (x-1) < 0的解集是( )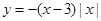 的递减区间是__________.
的递减区间是__________.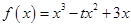 ,若对于任意的
,若对于任意的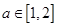 ,
,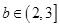 ,函数
,函数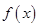 在区间
在区间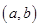 上单调递减,则实数
上单调递减,则实数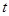 的取值范围是( )
的取值范围是( )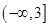
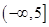
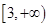

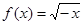
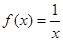
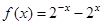
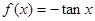
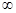 )上是增函数的是( )
)上是增函数的是( )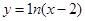
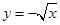
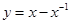
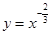
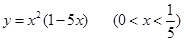 的最大值是
的最大值是 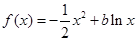 在
在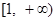 上是减函数,则
上是减函数,则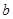 的取值范围是( )
的取值范围是( )