题目内容
直线a、b、c及平面α、β,下列命题正确的是( )
A.若a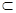 α,b α,b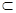 α,c⊥a, c⊥b 则c⊥α α,c⊥a, c⊥b 则c⊥α | B.若b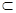 α, a//b则 a//α α, a//b则 a//α |
| C.若a//α,α∩β=b则a//b | D.若a⊥α, b⊥α 则a//b |
D
解析试题分析:A中a,b可能是平行直线,所以得不出c⊥α;B中可能a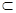 α,所以得不出a//α;C中a//α,但是a与α内的直线的位置关系不确定,所以得不出a//b;由线面垂直的性质定理知D正确.
α,所以得不出a//α;C中a//α,但是a与α内的直线的位置关系不确定,所以得不出a//b;由线面垂直的性质定理知D正确.
考点:本小题主要考查空间中直线与直线、直线与平面的位置关系,考查学生的空间想象能力和思维的严密性.
点评:要正确解决这类题目,就要准确掌握空间中线线、线面之间的平行、垂直的判定定理与性质定理并且灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正方体的一条对角线与正方体的棱可组成n对异面直线,则n等于 ( )
| A.2 | B.3 | C.6 | D.12 |
在正方体ABCD—A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于( ) 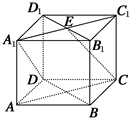
| A.AC | B.BD | C.A1D | D.A1D |
已知直线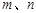 与平面
与平面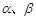 ,给出下列三个命题:
,给出下列三个命题:
①若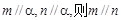 ②若
②若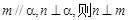
③若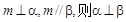 ④
④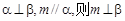
其中真命题的是( )
| A.②③ | B.②③④ | C.②③④ | D.①④ |
( )已知两个不同的平面 、
、 ,能判定
,能判定 //
// 的条件是
的条件是
A. 、 、 分别平行于直线 分别平行于直线 | B. 、 、 分别垂直于直线 分别垂直于直线 |
C. 、 、 分别垂直于平面 分别垂直于平面 | D. 内有两条直线分别平行于 内有两条直线分别平行于 |
如图,在透明塑料制成的长方体 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边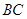 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
①水的部分始终呈棱柱状;
②水面四边形 的面积不改变;
的面积不改变;
③棱 始终与水面
始终与水面 平行;
平行;
④当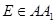 时,
时,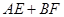 是定值.
是定值.
其中所有正确的命题的序号是( )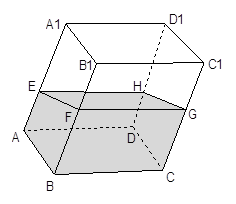
| A.①②③ | B.①③ | C.②④ | D.①③④ |
如图,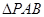 所在的平面
所在的平面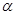 和四边形
和四边形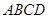 所在的平面
所在的平面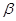 互相垂直,且
互相垂直,且 ,
,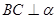 ,
,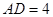 ,
,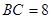 ,
,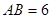 .若
.若 ,则动点
,则动点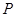 在平面
在平面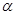 内的轨迹是
内的轨迹是 
| A.椭圆的一部分 | B.线段 | C.双曲线的一部分 | D.以上都不是 |
设 是三条不同的直线,
是三条不同的直线, 是两个不同的平面,则能使
是两个不同的平面,则能使 成立是( )
成立是( )
A. | B. |
C. | D. |
 =
= =
= ,则( )
,则( )