题目内容
1.已知函数f(x)=1-$\frac{a}{x}$+ln$\frac{1}{x}$(a为实数),当a=1时,求函数f(x)的图形在点($\frac{1}{2}$,f($\frac{1}{2}$))处的切线方程.分析 求出原函数的导函数,得到f′($\frac{1}{2}$)=2,然后由直线方程的点斜式得曲线在点($\frac{1}{2}$,f($\frac{1}{2}$))处的切线方程.
解答 解:由题意,f′(x)=$\frac{1}{{x}^{2}}$-$\frac{1}{x}$
∴f′($\frac{1}{2}$)=2,
即曲线在点x=$\frac{1}{2}$处的切线的斜率为2.
∵f($\frac{1}{2}$)=-1+ln2
∴曲线在点($\frac{1}{2}$,f($\frac{1}{2}$))处的切线方程为y+1-ln2=2×(x-$\frac{1}{2}$),
整理得:2x-y-2+ln2=0.
点评 本题考查利用导数研究曲线上某点处的切线方程,曲线在某点处的切线的斜率,就是函数在该点处的导数值,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.函数f(x)=x2+ax+2在区间[1,5]上至少有一个零点,则实数a的取值范围为( )
| A. | (-∞,-2$\sqrt{2}$] | B. | [-3,-2$\sqrt{2}$] | C. | [-$\frac{27}{5}$,-2$\sqrt{2}$] | D. | (-∞,-2$\sqrt{2}$]∪[2$\sqrt{2}$,+∞) |
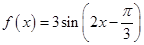 的图象为
的图象为 ,下列结论中正确的是( )
,下列结论中正确的是( ) 对称
对称 对称
对称 在区间
在区间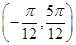 上递增
上递增 的图象向右平移
的图象向右平移 个单位长度可得
个单位长度可得 中,角
中,角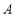 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, 满足
满足 ,
, ,
,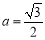 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.