题目内容
2.数列{an}满足a1=$\frac{1}{2}$,an+1an-2an+1+1=0(n∈N*)(Ⅰ)求证:数列{$\frac{1}{{a}_{n}-1}$}是等差数列;
(Ⅱ)求证:$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$>n+2-2$\sqrt{n+2}$.
分析 (Ⅰ)利用$\frac{1}{{a}_{n+1}-1}$-$\frac{1}{{a}_{n}-1}$化简、计算即得结论;
(Ⅱ)通过(I)可知an=$\frac{n}{n+1}$,利用数学归纳法证明即可.
解答 证明:(Ⅰ)∵an+1an-2an+1+1=0,
∴an+1an+1=2an+1,
∴$\frac{1}{{a}_{n+1}-1}$-$\frac{1}{{a}_{n}-1}$=$\frac{{(a}_{n}-1)-({a}_{n+1}-1)}{{a}_{n+1}{a}_{n}-{a}_{n}-{a}_{n+1}+1}$=$\frac{{a}_{n}-{a}_{n+1}}{2{a}_{n+1}-{a}_{n}-{a}_{n+1}}$=$\frac{{a}_{n}-{a}_{n+1}}{{a}_{n+1}-{a}_{n}}$=-1,
又∵a1=$\frac{1}{2}$,
∴$\frac{1}{{a}_{1}-1}$=$\frac{1}{\frac{1}{2}-1}$=-2,
∴数列{$\frac{1}{{a}_{n}-1}$}是以-2为首项、-1为公差的等差数列;
(Ⅱ)由(I)可知$\frac{1}{{a}_{n}-1}$=-2+(n-1)•(-1)=-n-1,
∴an=1+$\frac{1}{-n-1}$=$\frac{n}{n+1}$,
下面用数学归纳法来证明:$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$>n+2-2$\sqrt{n+2}$.
①当n=1时,左边=$\sqrt{{a}_{1}}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$>0,右边=1+2-2$\sqrt{1+2}$=3-2$\sqrt{3}$<0,结论成立;
②假设当n=k时,结论成立,即:$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{k}}$>k+2-2$\sqrt{k+2}$,
则当n=k+1时,在上式两边同时加上$\sqrt{\frac{k+1}{k+2}}$,得:
$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{k}}$+$\sqrt{\frac{k+1}{k+2}}$>k+2-2$\sqrt{k+2}$+$\sqrt{\frac{k+1}{k+2}}$,
下面用分析法证明:k+2-2$\sqrt{k+2}$+$\sqrt{\frac{k+1}{k+2}}$>(k+1)+2-2$\sqrt{k+3}$,
即证:-2$\sqrt{k+2}$+$\sqrt{\frac{k+1}{k+2}}$>1-2$\sqrt{k+3}$,
即证:2$\sqrt{k+3}$-2$\sqrt{k+2}$+$\sqrt{\frac{k+1}{k+2}}$>1,
即:2$\sqrt{(k+3)(k+2)}$-2(k+2)+$\sqrt{k+1}$>$\sqrt{k+2}$,
即:2$\sqrt{{k}^{2}+5k+6}$+$\sqrt{k+1}$>2k+4+$\sqrt{k+2}$,
而2$\sqrt{{k}^{2}+5k+6}$+$\sqrt{k+1}$>2$\sqrt{(k+\frac{9}{4})^{2}}$+$\sqrt{k+1}$
=2k+$\frac{9}{2}$+$\sqrt{k+1}$
=(2k+4)+($\frac{1}{2}$+$\sqrt{k+1}$)
=(2k+4)+$\frac{1+2\sqrt{k+1}}{2}$
=(2k+4)+$\frac{\sqrt{(1+2\sqrt{k+1})^{2}}}{2}$
=(2k+4)+$\frac{\sqrt{1+4k+4+4\sqrt{k+1}}}{2}$
>(2k+4)+$\frac{\sqrt{4k+8}}{2}$
=2k+4+$\sqrt{k+2}$,
由分析法原理可知2$\sqrt{{k}^{2}+5k+6}$+$\sqrt{k+1}$>2k+4+$\sqrt{k+2}$,
即当n=k+1时,结论也成立;
综上所述,$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$>n+2-2$\sqrt{n+2}$.
点评 本题是一道关于数列与不等式的综合题,考查等差数列的判定,考查数学归纳法,注意解题方法的积累,属于中档题.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | x2+y2+4x+4y+6=0 | B. | x2+y2-4x+4y+6=0 | C. | x2+y2-4x-4y+6=0 | D. | x2+y2+4x-4y+6=0 |
 中,角
中,角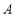 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, 满足
满足 ,
, ,
,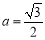 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.