题目内容
已知函数 .
.
(1)证明: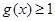 ;
;
(2)证明: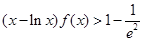 .
.
 .
.(1)证明:
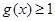 ;
;(2)证明:
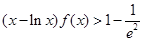 .
.(1)证明过程详见解析;(2)证明过程详见解析.
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,对函数
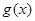 求导,利用
求导,利用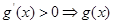 单调递增,
单调递增,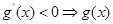 单调递减,来判断函数的单调性来决定函数最值的位置;第二问,因为
单调递减,来判断函数的单调性来决定函数最值的位置;第二问,因为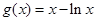 ,所以
,所以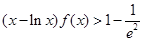 转化为
转化为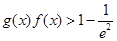 ,结合第一问的结论
,结合第一问的结论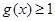 ,所以只需证明
,所以只需证明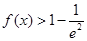 ,通过对
,通过对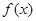 求导即可.
求导即可.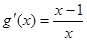 , 1分
, 1分当
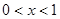 时,
时,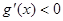 ,当
,当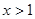 时,
时,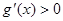
即
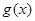 在
在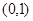 上为减函数,在
上为减函数,在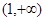 上为增函数 4分
上为增函数 4分∴
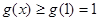 ,得证. 5分
,得证. 5分(2)
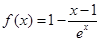 ,
,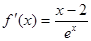 , 6分
, 6分∴
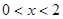 时,
时,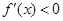 ,
,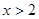 时,
时,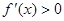
即
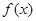 在
在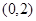 上为减函数,在
上为减函数,在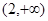 上为增函数
上为增函数∴
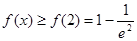 8分
8分又由(1)
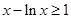 10分
10分∴
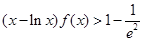 . 12分
. 12分
练习册系列答案
相关题目
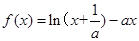 ,其中
,其中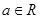 且
且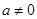 .
.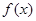 的单调性;
的单调性;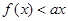 恒成立,求实数
恒成立,求实数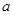 取值范围;
取值范围;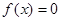 存在两个异号实根
存在两个异号实根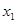 ,
,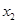 ,求证:
,求证: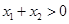
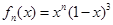 在
在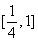 上的最大值为
上的最大值为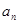 (
(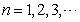 ).
).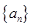 的通项公式;
的通项公式;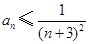 成立;
成立;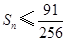 成立.
成立.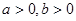 ,且函数
,且函数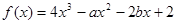 在
在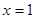 处有极值,则ab的最大值为 .
处有极值,则ab的最大值为 .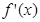 是函数
是函数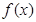 的导函数,将
的导函数,将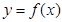 和
和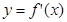 的图像画在同一个直角坐标系中,不可能正确的是( )
的图像画在同一个直角坐标系中,不可能正确的是( )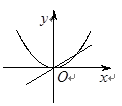
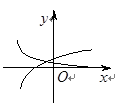
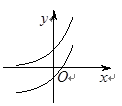
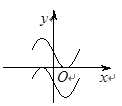
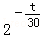 ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )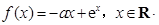
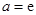 ,求函数
,求函数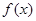 的单调区间;
的单调区间;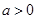 ,且对于任意
,且对于任意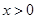 不等式
不等式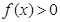 恒成立,试确定实数
恒成立,试确定实数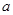 的取值范围;
的取值范围;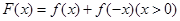 ,求证:
,求证: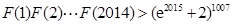
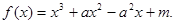
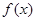 在
在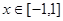 内没有极值点,求
内没有极值点,求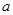 的取值范围;
的取值范围;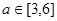 ,不等式
,不等式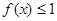 在
在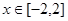 上恒成立,求实数
上恒成立,求实数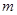 的取值范围.
的取值范围.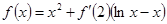 ,则
,则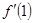 = ( )
= ( )