题目内容
(本小题满分14分)已知点P(2,0),及圆C:x2+y2-6x+4y+4=0.
(1)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(2)设过点P的直线与圆C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
(1)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(2)设过点P的直线与圆C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
(1)x=2;(2)(x-2)2+y2=4
本试题主要是考查了直线与圆的位置关系的运用。以及圆的方程的求解问题。
(1)因为设直线l的斜率为k(k存在)则方程为y-0=k(x-2)
又⊙C的圆心为(3,-2) ,r=3,利用线与圆的位置关系可知直线的方程。
(2)根据设过点P的直线与圆C交于A、B两点,当|AB|=4,利用半径长和半弦长,弦心距的勾股定理得到结论。
解:(1)设直线l的斜率为k(k存在)则方程为y-0=k(x-2) …………………1分
又⊙C的圆心为(3,-2) ,r=3
由 ……………………4分
……………………4分
所以直线方程为 ……………………6分
……………………6分
当k不存在时,l的方程为x=2. ……………………8分
(2)由弦心距 , ……………………11分
, ……………………11分
知P为AB的中点,故以AB为直径的圆的方程为(x-2)2+y2=4. …………………14分
(1)因为设直线l的斜率为k(k存在)则方程为y-0=k(x-2)
又⊙C的圆心为(3,-2) ,r=3,利用线与圆的位置关系可知直线的方程。
(2)根据设过点P的直线与圆C交于A、B两点,当|AB|=4,利用半径长和半弦长,弦心距的勾股定理得到结论。
解:(1)设直线l的斜率为k(k存在)则方程为y-0=k(x-2) …………………1分
又⊙C的圆心为(3,-2) ,r=3
由
 ……………………4分
……………………4分所以直线方程为
 ……………………6分
……………………6分当k不存在时,l的方程为x=2. ……………………8分
(2)由弦心距
 , ……………………11分
, ……………………11分知P为AB的中点,故以AB为直径的圆的方程为(x-2)2+y2=4. …………………14分

练习册系列答案
相关题目
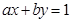 与圆
与圆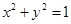 没有交点,则
没有交点,则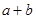 的取值范围
的取值范围 上任意一点,则△ABC面积的最小值是______________.
上任意一点,则△ABC面积的最小值是______________.  的圆心与点
的圆心与点 关于直线
关于直线 对称,并且圆
对称,并且圆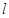 与圆
与圆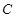 相交于点
相交于点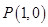 和点
和点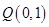 。
。 ,则l的方程为( )
,则l的方程为( ) 、
、 的极坐标方程分别为
的极坐标方程分别为 ,
, ,则曲线
,则曲线 和圆
和圆 关于直线
关于直线 对称,过点
对称,过点 的圆
的圆 与
与 轴相切,则圆心
轴相切,则圆心

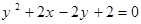

 关于直线
关于直线
 对称,则
对称,则 的取值范围是( )
的取值范围是( ) ]
]