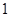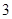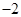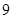题目内容
.已知曲线 、
、 的极坐标方程分别为
的极坐标方程分别为 ,
, ,则曲线
,则曲线 上的点与曲线
上的点与曲线 上的点的最远距离为
上的点的最远距离为
 、
、 的极坐标方程分别为
的极坐标方程分别为 ,
, ,则曲线
,则曲线 上的点与曲线
上的点与曲线 上的点的最远距离为
上的点的最远距离为 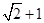
解:曲线C1的极坐标方程分别为ρ=-2cos(θ+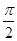 )
)
即ρ=2sinθ,两边同乘以ρ,得ρ2=2ρsinθ,
化为普通方程为x2+y2=2y,即x2+(y-1)2=1.
表示以C(0,1)为圆心,半径为1 的圆.
C2的极坐标方程分别为 2 ρcos(θ-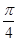 )+1=0,
)+1=0,
即ρsinθ+ρcosθ+1=0,
化为普通方程为x+y+1=0,表示一条直线.
如图,圆心到直线距离d=|CQ|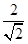 =
= 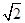 曲线C1上的点与曲线C2上的点的最远距离为|PQ|="d+r="
曲线C1上的点与曲线C2上的点的最远距离为|PQ|="d+r=" 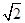 +1
+1
故答案为: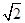 +1,
+1,
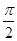 )
)即ρ=2sinθ,两边同乘以ρ,得ρ2=2ρsinθ,
化为普通方程为x2+y2=2y,即x2+(y-1)2=1.
表示以C(0,1)为圆心,半径为1 的圆.
C2的极坐标方程分别为 2 ρcos(θ-
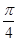 )+1=0,
)+1=0,即ρsinθ+ρcosθ+1=0,
化为普通方程为x+y+1=0,表示一条直线.
如图,圆心到直线距离d=|CQ|
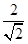 =
= 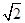 曲线C1上的点与曲线C2上的点的最远距离为|PQ|="d+r="
曲线C1上的点与曲线C2上的点的最远距离为|PQ|="d+r=" 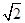 +1
+1故答案为:
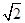 +1,
+1,
练习册系列答案
相关题目
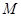 (1,3),与直线x+2y-7=0相切.
(1,3),与直线x+2y-7=0相切. 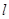 :
: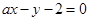
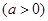 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数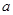 的取值范围;
的取值范围;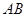 的垂直平分线过点
的垂直平分线过点 , 若存在,求出实数
, 若存在,求出实数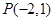 且被圆C:
且被圆C: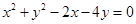 截得弦最长的直线l的方程是( )
截得弦最长的直线l的方程是( ) 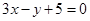
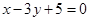
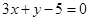
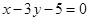
 上两点
上两点 关于直线
关于直线 对称,则圆
对称,则圆 的半径为
的半径为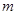 、
、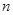 ,则直线
,则直线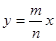 与圆
与圆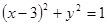 相交的概率是( )
相交的概率是( )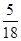
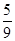
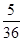
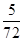
 (
( 为参数)的倾斜角的大小.
为参数)的倾斜角的大小.  ,
, 是曲线
是曲线 上任意一点,求
上任意一点,求 的面积的最小值.
的面积的最小值.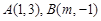 ,直线
,直线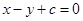 将这两圆的面积均平分,则
将这两圆的面积均平分,则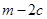 的值是( )
的值是( )