题目内容
10.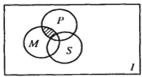 如图,全集U={1,2,3,4,5,8,9},M={2,3,5,8}.P={1,3,5,8,9}.S={2,3,8}是U的3个子集,则阴影部分所表示的集合等于( )
如图,全集U={1,2,3,4,5,8,9},M={2,3,5,8}.P={1,3,5,8,9}.S={2,3,8}是U的3个子集,则阴影部分所表示的集合等于( )| A. | 2,5,8 | B. | {2,5,8} | C. | 5 | D. | {5} |
分析 观察阴影部分所表示的集合中元素的特点,它具有在集合P和M中,不在集合S中,利用集合元素的含义即可解决.
解答 解:依题意,由图知,
阴影部分对应的元素a具有性质a∈M,a∈P,a∈CUS,
所以阴影部分所表示的集合是(M∩P)∩CUS,
全集U={1,2,3,4,5,8,9},M={2,3,5,8}.P={1,3,5,8,9}.S={2,3,8}
故(M∩P)∩CUS={3,5,8}∩{1,4,5,6,7,9}={5}.
故选:D.
点评 本题主要考查了Venn图表达集合的关系及运算,属于基础题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
1.若f(x)=sinx+cosx,f′(x)是f(x)的导函数,要得到g(x)=$\sqrt{2}f(x){f}^{′}$(x)的图象,需将f(2x)的图象( )
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向右平移 $\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
18.已知f(x)=sin(x+$\frac{π}{2}$),g(x)=cos(x-$\frac{π}{2}$),则f(x)的图象( )
| A. | 与g(x)的图象相同 | |
| B. | 与g(x)的图象关于y轴对称 | |
| C. | 是由g(x)的图象向左平移$\frac{π}{2}$个单位得到的 | |
| D. | 是由g(x)的图象向右平移$\frac{π}{2}$个单位得到的 |
15.下列区间是函数y=2|cosx|的单调递减区间的是( )
| A. | (0,π) | B. | (-$\frac{π}{2}$,0) | C. | ($\frac{3π}{2}$,2π) | D. | (-π,-$\frac{π}{2}$) |
2.已知$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(x,x-1)且$\overrightarrow{a}$∥$\overrightarrow{b}$,则x等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |
19.函数f(x)=mx3-x+1在(-∞,+∞) 上是减函数的一个充分不必要条件是( )
| A. | m<0 | B. | m≤0 | C. | m≤1 | D. | m<1 |
20.i为虚数单位,已知复数z和(z+2)2+8i都是纯虚数,则复数1+$\overline{z}$( )
| A. | 1±2i | B. | 1+2i | C. | 1-2i | D. | ±2i |