题目内容
(本小题12分)如图,四棱椎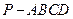 的底面为菱形,且
的底面为菱形,且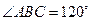 ,
,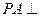 平面
平面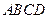 ,
,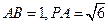 ,
,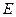 为
为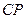 的中点.
的中点.
(1)求直线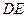 与平面
与平面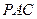 所成角的正切值;
所成角的正切值;
(2)在线段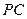 上是否存在一点
上是否存在一点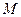 ,使
,使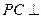 面
面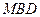 成立?如果存在,求出
成立?如果存在,求出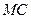 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.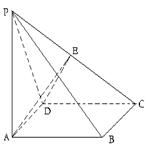
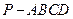 的底面为菱形,且
的底面为菱形,且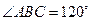 ,
,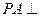 平面
平面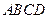 ,
,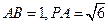 ,
,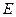 为
为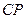 的中点.
的中点.(1)求直线
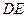 与平面
与平面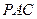 所成角的正切值;
所成角的正切值;(2)在线段
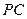 上是否存在一点
上是否存在一点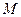 ,使
,使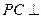 面
面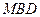 成立?如果存在,求出
成立?如果存在,求出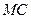 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
(1)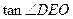 =
=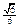
(2)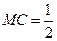
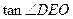 =
=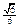
(2)
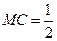
(1)如图,连结
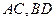 交于点
交于点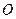 ,
,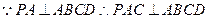 ,又
,又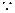 底面
底面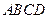 是菱形,
是菱形,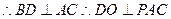 ,连结
,连结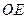 ,则
,则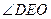 为
为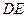 与平面
与平面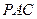 所成的角,所以
所成的角,所以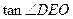 =
=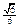
(2)过点
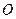 作
作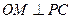 于
于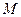 ,由
,由
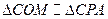 得
得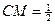 ,因为
,因为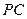 在底面
在底面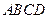 上的射影为
上的射影为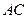 且
且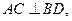 所以
所以 ,又
,又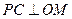 ,所以
,所以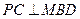
所以,所求
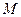 存在,且使
存在,且使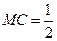 。
。
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
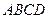 是边长为
是边长为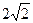 的正方形,
的正方形,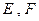 分别为
分别为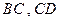 的中点,沿
的中点,沿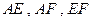 将
将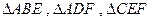 向同侧折叠且与平面
向同侧折叠且与平面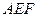 成直二面角,连接
成直二面角,连接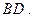
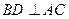 ;
;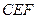 与平面
与平面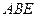 所成锐角的余弦值。
所成锐角的余弦值。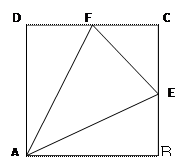

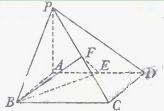
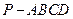 的底面是边长为2的正方形,
的底面是边长为2的正方形, 面
面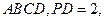
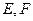 分别为
分别为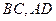 的中点.
的中点.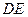 与面
与面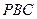 所成的角;
所成的角;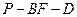 的大小.
的大小.

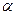 、
、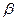 是两个不同平面,
是两个不同平面,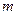 、
、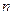 是两不同直线,下列命题中的假命题是 ( )
是两不同直线,下列命题中的假命题是 ( )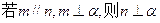
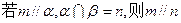
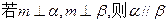
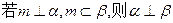
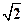 ,
,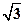 ,
,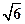 ,这个长方体对角线的长是( )
,这个长方体对角线的长是( )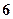
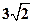
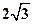
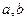 ,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为
,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为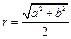 ”. 对于“若三棱锥三条侧棱两两垂直,侧棱长分别为
”. 对于“若三棱锥三条侧棱两两垂直,侧棱长分别为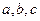 ”,类比上述处理方法,可得该三棱锥的外接球半径为
”,类比上述处理方法,可得该三棱锥的外接球半径为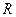 = ▲ .
= ▲ .