题目内容
16.已知函数y=f(x2-1)的定义域为[-$\sqrt{3}$,$\sqrt{3}$],则函数y=f(x)的定义域是[-1,2].分析 根据复合函数定义域之间的关系进行求解即可.
解答 解:∵函数y=f(x2-1)的定义域为[-$\sqrt{3}$,$\sqrt{3}$],
∴-$\sqrt{3}$≤x≤$\sqrt{3}$,
即0≤x2≤3,
-1≤x2-1≤2,
即函数y=f(x)的定义域为[-1,2],
故答案为:[-1,2]
点评 本题主要考查函数的定义域的求解,要求熟练掌握复合函数定义域之间的关系.

练习册系列答案
相关题目
8.下面列举的图形一定是平面图形的是( )
| A. | 有一个角是直角的四边形 | B. | 有两个角是直角的四边形 | ||
| C. | 有三个角是直角的四边形 | D. | 有四个角是直角的四边形 |
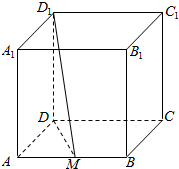 如图所示,正方体ABCD-A1B1C1D1的棱长为1,M是AB的中点,求D1M与面ABCD所成角的正切值.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,M是AB的中点,求D1M与面ABCD所成角的正切值.