题目内容
20.执行如图所示的程序框图,则输出s的值为( )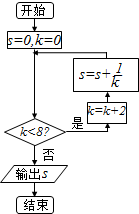
| A. | $\frac{25}{24}$ | B. | $\frac{11}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
分析 根据已知的框图,可知程序的功能是利用循环累加循环变量$\frac{1}{k}$的值到累加变量S,并在循环变量k值大于等于8时,输出累加结果.
解答 解:模拟执行程序框图,可得
s=0,k=0
满足条件k<8,k=2,s=$\frac{1}{2}$,
满足条件k<8,k=4,s=$\frac{1}{2}$+$\frac{1}{4}$,
满足条件k<8,k=6,s=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$,
满足条件k<8,k=8,s=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$=$\frac{25}{24}$,
不满足条件k<8,退出循环,输出s的值为$\frac{25}{24}$.
故选:A.
点评 本题考查的知识点是程序框图,当程序的运行次数不多时,我们多采用模拟程序运行的方法得到程序的运行结果.

练习册系列答案
相关题目
15.已知过原点的直线l与曲线C:$\frac{{x}^{2}}{3}$+y2=1相交,直线l被曲线C所截得的线段长等于$\sqrt{6}$,则直线l的斜率k的-个取值是 ( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $-\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 1 |
12.已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x-2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$,设a=f(-5),b=f($\frac{19}{2}$),c=f($\frac{41}{4}$),则a,b,c的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | b<c<a | D. | a<b<c |
9.某人射击一次命中目标的概率为$\frac{1}{2}$,则此人射击6次,3次命中且恰有2次连续命中的概率为( )
| A. | C${\;}_{6}^{3}$($\frac{1}{2}$)6 | B. | A${\;}_{4}^{2}$($\frac{1}{2}$)6 | C. | C${\;}_{4}^{2}$($\frac{1}{2}$)6 | D. | C${\;}_{4}^{1}$($\frac{1}{2}$)6 |