题目内容
12.已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x-2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$,设a=f(-5),b=f($\frac{19}{2}$),c=f($\frac{41}{4}$),则a,b,c的大小关系是( )| A. | b<a<c | B. | c<a<b | C. | b<c<a | D. | a<b<c |
分析 由题意可得函数y=f(x)为周期为4的函数,从而可得c=f($\frac{41}{4}$)=f($\frac{9}{4}$)=f($\frac{7}{4}$),b=f($\frac{19}{2}$)=f($\frac{3}{2}$),利用函数y=f(x+2)是偶函数,可得a=f(-5)=f(3)=f(1),利用单调性即可求解.
解答 解:∵对于任意的x∈R,都有f(x+2)=f(x-2),
∴f(x+4)=f(x),故函数y=f(x)为周期为4的函数.
∴b=f($\frac{19}{2}$)=f($\frac{3}{2}$),
∵函数y=f(x+2)是偶函数
∴f(-x+2)=f(x+2),
∴a=f(-5)=f(3)=f(1),c=f($\frac{41}{4}$)=f($\frac{9}{4}$)=f($\frac{7}{4}$),
∵当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$是增函数,1<$\frac{3}{2}$<$\frac{7}{4}$,
∴a<b<c.
故选:D.
点评 本题主要考查函数值的计算,根据函数奇偶性和周期性进行转化是解决本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
3.已知f(x)是定义在R上的奇函数,当x<0时,f(x)=x2+2x,则函数$g(x)=f(x)+\frac{1}{2}x-1$零点的集合为( )
| A. | {1,-1,0} | B. | {-2,2,0} | C. | $\{2,-\frac{1}{2},\frac{{-5+\sqrt{41}}}{4}\}$ | D. | $\{2,\frac{1}{2},\frac{{-5-\sqrt{41}}}{4}\}$ |
20.执行如图所示的程序框图,则输出s的值为( )
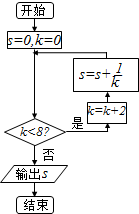

| A. | $\frac{25}{24}$ | B. | $\frac{11}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |
2.下面结论中,不正确的是( )
| A. | 若a>1,则函数y=ax与y=logax在定义域内均为增函数 | |
| B. | 函数y=3x与y=log3x图象关于直线y=x对称 | |
| C. | $y={log_a}{x^2}$与y=2logax表示同一函数 | |
| D. | 若0<a<1,0<m<n<1,则一定有logam>logan>0 |