题目内容
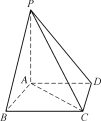
【题目】已知三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,设点
,设点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 上一点,且
上一点,且![]() .
.
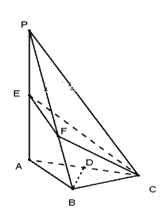
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,通过证
,通过证![]() ,并说明
,并说明![]() 平面
平面![]() ,来证明
,来证明![]() 平面
平面![]()
(2)采用建系法以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别表示出对应的点
,分别表示出对应的点![]() 坐标,设平面
坐标,设平面![]() 的一个法向量为
的一个法向量为![]() ,结合直线对应的
,结合直线对应的![]() 和法向量
和法向量![]() ,利用向量夹角的余弦公式进行求解即可
,利用向量夹角的余弦公式进行求解即可
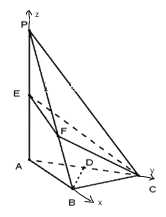
![]() 证明:如图,
证明:如图,
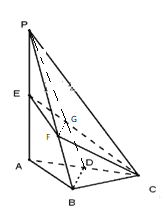
连接![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,
,![]() 点
点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,
的中点,
![]() 点
点![]() 为
为![]() 的重心,则
的重心,则![]() ,
,![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,可得
,可得![]() ,又
,又![]() ,
,
则以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由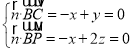 ,
,
取![]() ,得
,得![]() .设直线
.设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() .
.![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
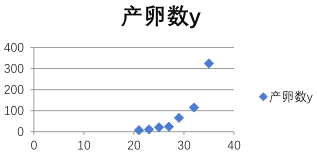
【题目】只红铃虫的产卵数y和温度x有关,现收集了7组观测数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
27 | 81 | 3.6 | 152 | 2936 | 38 |
其中![]()
(1)根据散点图判断,![]() 与
与![]() (e为自然对数的底数
(e为自然对数的底数![]() )哪一个更适宜作为红铃虫的产卵数y和温度x的回归方程类型?(给出判断即可,不必说明理由)
)哪一个更适宜作为红铃虫的产卵数y和温度x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)根据(2)的结果,当温度为37度时红铃虫的产卵数y的预报值是多少?
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其线性回归方程
,其线性回归方程![]() 的系数的最小二乘法估计值为
的系数的最小二乘法估计值为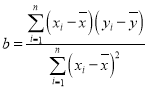 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]()