Question

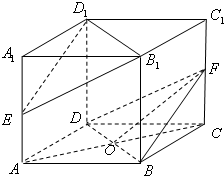如图，在正方体ABCD-A₁B₁C₁D₁ 中，E、F分别为棱AA₁、CC₁的中点，O是AC，BD的交点．
（1）证明：B₁D₁⊥OF； 
（2）证明：平面EB₁D₁∥平面BDF．

Answer 1

分析：（1）先证明OF⊥BD，再证明B₁D₁∥BD，即可得到结论；
（2）证明线面平行，即ED₁∥平面EB₁D₁，即可证明平面EB₁D₁∥平面BDF．

解答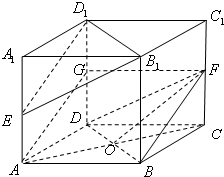：证明：（1）∵ABCD-A₁B₁C₁D₁ 是正方体
∴DF=BF，O是AC的中点，∴OF⊥BD
又∵BB₁∥DD₁，∴BB₁D₁D是平行四边形
∴B₁D₁∥BD，∴B₁D₁⊥OF…（6分）
（2）由（1）知B₁D₁∥BD，而B₁D₁?平面EB₁D₁，BD?平面EB₁D₁
∴BD∥平面EB₁D₁
取DD₁中点G，连接FG，∴FG∥AB且GF=AB
∴ABFG是平行四边形，∴AG∥BF
又∵AE∥GD₁且AE=GD₁，∴EAGD₁是平行四边形
∴AG∥ED₁，ED₁∥BF
而ED₁?平面EB₁D₁，BF?平面EB₁D₁，∴ED₁∥平面EB₁D₁
又ED₁∩B₁D₁=D₁，ED₁，B₁D₁?平面EB₁D₁
∴平面EB₁D₁∥平面BDF．…（14分）

点评：本题考查线线垂直，考查面面平行，考查学生分析解决问题的能力，属于中档题．