题目内容
13.若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点,则p=2$\sqrt{2}$.分析 先求出x2-y2=1的左焦点,得到抛物线y2=2px的准线,依据p的意义求出它的值.
解答 解:双曲线x2-y2=1的左焦点为(-$\sqrt{2}$,0),故抛物线y2=2px的准线为x=-$\sqrt{2}$,
∴$\frac{p}{2}$=$\sqrt{2}$,∴p=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题考查抛物线和双曲线的简单性质,以及抛物线方程 y2=2px中p的意义.

练习册系列答案
相关题目
4.已知复数z满足(z-1)i=1+i,则z=( )
| A. | -2-i | B. | -2+i | C. | 2-i | D. | 2+i |
8.“sinα=cosα”是“cos2α=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
18.sin20°cos10°-cos160°sin10°=( )
| A. | $-\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.
高三年级267位学生参加期末考试,某班37位学生的语文成绩,数学成绩与总成绩在全年级的排名情况如图所示,甲、乙、丙为该班三位学生.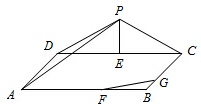 如图,三角形△PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3,点E是CD的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.
如图,三角形△PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3,点E是CD的中点,点F、G分别在线段AB、BC上,且AF=2FB,CG=2GB.