题目内容
已知函数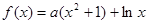 .
.
(Ⅰ)讨论函数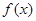 的单调性;
的单调性;
(Ⅱ)若对任意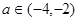 及
及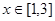 时,恒有
时,恒有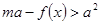 成立,求实数
成立,求实数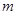 的取值范围.
的取值范围.
(1)当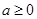 时,
时,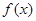 在
在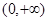 上是增函数;当
上是增函数;当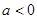 时,
时,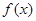 在
在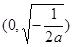 上是增函数,
上是增函数,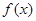 在
在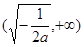 上是减函数.
上是减函数.
(2)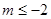
解析试题分析:解: (Ⅰ) 2分
2分
①当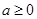 时,恒有
时,恒有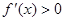 ,则
,则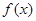 在
在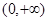 上是增函数; 4分
上是增函数; 4分
②当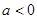 时,当
时,当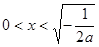 时,
时,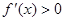 ,则
,则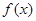 在
在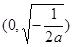 上是增函数;
上是增函数;
当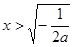 时,
时,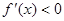 ,则
,则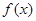 在
在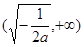 上是减函数 6分
上是减函数 6分
综上,当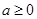 时,
时,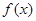 在
在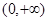 上是增函数;当
上是增函数;当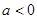 时,
时,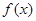 在
在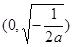 上是增函数,
上是增函数,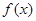 在
在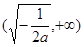 上是减函数. 7分
上是减函数. 7分
(Ⅱ)由题意知对任意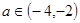 及
及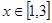 时,
时,
恒有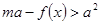 成立,等价于
成立,等价于
因为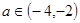 ,所以
,所以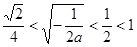
由(Ⅰ)知:当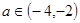 时,
时,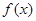 在
在 上是减函数
上是减函数
所以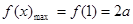 10分
10分
所以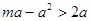 ,即
,即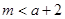
因为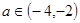 ,所以
,所以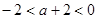
所以实数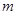 的取值范围为
的取值范围为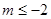 12分
12分
考点:导数的运用
点评:主要是考查了导数在研究函数中的运用,属于基础题。

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 ,其中
,其中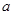 为大于零的常数,
为大于零的常数,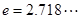 ,函数
,函数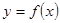 的图像与坐标轴交点处的切线为
的图像与坐标轴交点处的切线为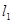 ,函数
,函数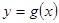 的图像与直线
的图像与直线 交点处的切线为
交点处的切线为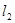 ,且
,且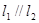 .
.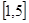 上存在
上存在 使不等式
使不等式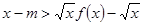 成立,求实数
成立,求实数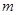 的取值范围;
的取值范围;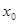 ,我们把
,我们把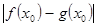 的值称为两函数在
的值称为两函数在 千件,需另投入成本为
千件,需另投入成本为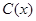 ,当年产量不足80千件时,
,当年产量不足80千件时,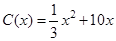 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,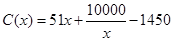 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.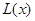 (万元)关于年产量
(万元)关于年产量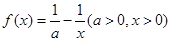
 在
在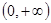 上的单调;
上的单调;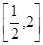 上的值域是
上的值域是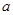 的值.
的值.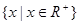 ,且f(x)为增函数,f(xy)=f(x)+f(y)。
,且f(x)为增函数,f(xy)=f(x)+f(y)。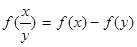 ;
;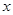 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米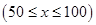 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油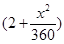 升,司机的工资是每小时14元.
升,司机的工资是每小时14元. 关于
关于