题目内容
(本小题满分14分) 设函数
设函数 ,且
,且 ,
, .求证:
.求证: (Ⅰ)
(Ⅰ) 且
且 ;
; (Ⅱ)方程
(Ⅱ)方程 在区间
在区间 内至少有一个根;
内至少有一个根; (Ⅲ)设
(Ⅲ)设 ,
, 是方程
是方程 的两个根,则
的两个根,则 .
.


 设函数
设函数 ,且
,且 ,
, .求证:
.求证: (Ⅰ)
(Ⅰ) 且
且 ;
; (Ⅱ)方程
(Ⅱ)方程 在区间
在区间 内至少有一个根;
内至少有一个根; (Ⅲ)设
(Ⅲ)设 ,
, 是方程
是方程 的两个根,则
的两个根,则 .
.


略
(Ⅰ)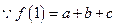 =
=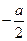 ,
,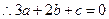 .又
.又 ,
,
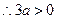 ,
,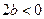 ,
,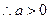 ,
,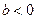 .
.
又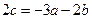 ,由
,由 ,
,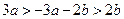 .
.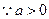 ,
, .
.
(Ⅱ)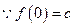 ,且
,且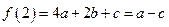 .
.
1当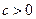 时,
时,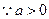 ,
,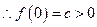 且
且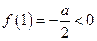 ,
,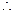 方程
方程 在区间
在区间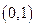 内至少有一根;
内至少有一根;
2当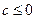 时,
时,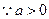 ,
,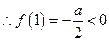 且
且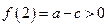 ,
,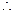 方程
方程 在区间
在区间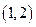 内至少又一个根.
内至少又一个根.
综合12得方程 在区间
在区间 内至少有一个根.
内至少有一个根.
(Ⅲ)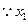 、
、 是方程
是方程 的两个根,
的两个根,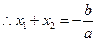 ,
,
所以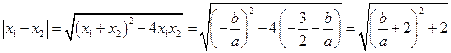 .
.
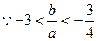 ,
,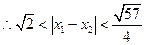 .
.
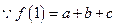 =
=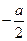 ,
,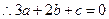 .又
.又 ,
,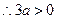 ,
,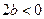 ,
,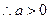 ,
,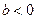 .
.又
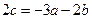 ,由
,由 ,
,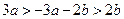 .
.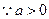 ,
, .
.(Ⅱ)
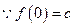 ,且
,且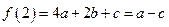 .
.1当
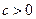 时,
时,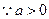 ,
,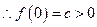 且
且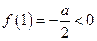 ,
,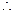 方程
方程 在区间
在区间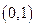 内至少有一根;
内至少有一根;2当
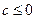 时,
时,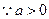 ,
,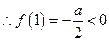 且
且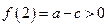 ,
,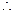 方程
方程 在区间
在区间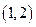 内至少又一个根.
内至少又一个根.综合12得方程
 在区间
在区间 内至少有一个根.
内至少有一个根.(Ⅲ)
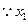 、
、 是方程
是方程 的两个根,
的两个根,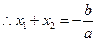 ,
,所以
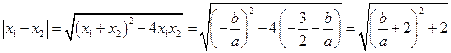 .
.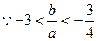 ,
,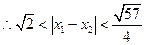 .
.
练习册系列答案
相关题目
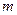 为何值时,关于
为何值时,关于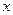 的方程
的方程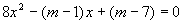 的两根:
的两根: ,直线
,直线 与
与
 上,则
上,则 。
。 是以
是以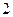 为周期的偶函数,当
为周期的偶函数,当 时,
时,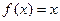 ,那么在区间
,那么在区间 内,关于
内,关于 的方程
的方程 (
( 且
且 )有
)有 个不同的根,则
个不同的根,则 的取值范围是( )
的取值范围是( )




 的一个零点在
的一个零点在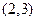 内,则实数
内,则实数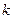 的取值范围是( )
的取值范围是( )