题目内容
【题目】[选修4-1:几何证明选讲]
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, ![]() OA为半径作圆.
OA为半径作圆.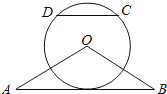
(1)证明:直线A与⊙O相切;
(2)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
【答案】
(1)
设圆的半径为r,作OK⊥AB于K,
∵OA=OB,∠AOB=120°,
∴OK⊥AB,∠A=30°,OK=OAsin30°= ![]() r,
r,
∴直线AB与⊙O相切;
(2)
点C,D在⊙O上,且A,B,C,D四点共圆,不妨设圆心为T,
∵OA=OB,TA=TB,
∴OT为AB的中垂线,
同理,OC=OD,TC=TD,
∴OT为CD的中垂线,
∴AB∥CD
【解析】(Ⅰ)过点O作OK⊥AB于点K.根据等腰三角形AOB的性质知OK⊥AB,∠A=30°,OK=OAsin30°= ![]() r,则AB是圆O的切线.
r,则AB是圆O的切线.
(2)设圆心为T,证明OT为AB的中垂线,OT为CD的中垂线,即可证明结论.;
本题考查了切线的判定,考查四点共圆,考查学生分析解决问题的能力.解答此题时,充分利用了等腰三角形“三合一”的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目