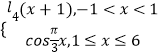题目内容
【题目】已知函数![]() 与
与![]() .
.
(1)若曲线![]() 与曲线
与曲线![]() 恰好相切于点
恰好相切于点![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求证:![]() .
. ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)先求出导函数![]() 由
由![]() ,解方程可得
,解方程可得![]() ;
;
(2)由 ![]() 在
在![]() 恒成立的必要条件为
恒成立的必要条件为![]() 得
得![]() ,再利用导数研究函数的单调性及最值,从而证明
,再利用导数研究函数的单调性及最值,从而证明![]() 时,对任意
时,对任意![]() ,总有
,总有![]() ;(3)由(2)知:
;(3)由(2)知:![]() 时
时![]() ,令
,令![]() ,化简可得
,化简可得![]() ,再令
,再令![]() ,多个不等式求和,利用对数的运算法则即可的结论.
,多个不等式求和,利用对数的运算法则即可的结论.
试题解析:(1)先求出导函数![]() 由
由![]() ,解方程可得
,解方程可得![]() .
.
(2)令![]() ,则
,则![]() ,
,![]() 在
在![]() 恒成立的必要条件为
恒成立的必要条件为![]() .即
.即![]() ,
,![]() 又当
又当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,
,![]() 在
在![]() 递减
递减![]() ,即
,即![]() ,
,![]() 在
在![]() 恒成立的充分条件为
恒成立的充分条件为![]() .综上,可得:
.综上,可得:![]()
(3)设![]() 为
为![]() 的前n项和,则
的前n项和,则![]() ,要证原不等式,只需证:
,要证原不等式,只需证:![]() ,由(2)知:
,由(2)知:![]() 时
时![]() 即:
即:![]() (当且仅当
(当且仅当![]() 时取等号).令
时取等号).令![]() ,则
,则![]() ,即:
,即:![]() ,即
,即![]() , 令
, 令![]() ,多个不等式求和,从而原不等式得证
,多个不等式求和,从而原不等式得证

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目