Question

【题目】已知函数f（x）=（x﹣t）|x|（t∈R）．
（1）当t=2时，求函数f（x）的单调性；
（2）试讨论函数f（x）的单调区间；
（3）若t∈（0，2），对于x∈[﹣1，2]，不等式f（x）＞x+a都成立，求实数a的取值范围．

Answer 1

【答案】
（1）解：当t=2时，f（x）=（x﹣t）|x|= ，

根据二次函数的图像与性质可得：

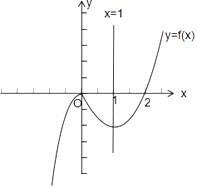
f（x）在（﹣∞，0）上单调递增，（0，1）上单调递减，（1，+∞）上单调递增．

（2）解：f（x）= ，

当t＞0时，f（x）的单调增区间为[ ，+∞），（﹣∞，0]，单调减区间为[0， ]，

当t=0时，f（x）的单调增区间为R

当t＜0时，f（x）的单调增区间为[0，+∞），（﹣∞， ]，单调减区间为[ ）

（3）解：设g（x）=f（x）﹣x= ，

x∈[0，2]时，∵ ∈（0，2），∴gmin（x）=g（ ）=﹣

x∈[﹣1，0]时，∵g（﹣1）=﹣t，g（0）=0，∴gmin（x）=﹣t

故只须t∈（0，2），使得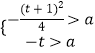： 成立，即 ．

所以a≤﹣

【解析】（1）当t=2时，f（x）=（x﹣t）|x|= ，作出其图像，利用二次函数的单调性可求函数f（x）的单调性；（2）分t＞0、t=0、t＜0三类讨论，可求得函数f（x）的单调区间；（3）设g（x）=f（x）﹣x= ，依题意，可求得gmin（x）=﹣t，只须t∈（0，2），使得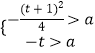： 成立，解之即可求得实数a的取值范围．
【考点精析】关于本题考查的奇偶性与单调性的综合，需要了解奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能得出正确答案．