题目内容
设函数f(x)= ,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
(1)求函数h(a)的解析式;
(2)画出函数y=h(x)的图象并指出h(x)的最小值.
 ,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).(1)求函数h(a)的解析式;
(2)画出函数y=h(x)的图象并指出h(x)的最小值.
(1)h(a)=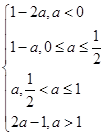
(2)见解析
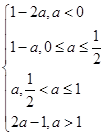
(2)见解析
解:(1)由题意知g(x)=
当a<0时,函数g(x)是[1,3]上的增函数,
此时g(x)max=g(3)=2-3a,
g(x)min=g(1)=1-a,
所以h(a)=1-2a;
当a>1时,函数g(x)是[1,3]上的减函数,
此时g(x)min=g(3)=2-3a,
g(x)max=g(1)=1-a,
所以h(a)=2a-1;
当0≤a≤1时,若x∈[1,2],
则g(x)=1-ax,有g(2)≤g(x)≤g(1);
若x∈(2,3],则g(x)=(1-a)x-1,
有g(2)<g(x)≤g(3),
因此g(x)min=g(2)=1-2a,
而g(3)-g(1)=(2-3a)-(1-a)=1-2a,
故当0≤a≤ 时,g(x)max=g(3)=2-3a,有h(a)=1-a;
时,g(x)max=g(3)=2-3a,有h(a)=1-a;
当 <a≤1时,g(x)max=g(1)=1-a,有h(a)=a.
<a≤1时,g(x)max=g(1)=1-a,有h(a)=a.
综上所述,h(a)=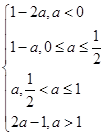
(2)画出y=h(x)的图象,如图所示,数形结合可得h(x)min=h( )=
)= .
.


当a<0时,函数g(x)是[1,3]上的增函数,
此时g(x)max=g(3)=2-3a,
g(x)min=g(1)=1-a,
所以h(a)=1-2a;
当a>1时,函数g(x)是[1,3]上的减函数,
此时g(x)min=g(3)=2-3a,
g(x)max=g(1)=1-a,
所以h(a)=2a-1;
当0≤a≤1时,若x∈[1,2],
则g(x)=1-ax,有g(2)≤g(x)≤g(1);
若x∈(2,3],则g(x)=(1-a)x-1,
有g(2)<g(x)≤g(3),
因此g(x)min=g(2)=1-2a,
而g(3)-g(1)=(2-3a)-(1-a)=1-2a,
故当0≤a≤
 时,g(x)max=g(3)=2-3a,有h(a)=1-a;
时,g(x)max=g(3)=2-3a,有h(a)=1-a;当
 <a≤1时,g(x)max=g(1)=1-a,有h(a)=a.
<a≤1时,g(x)max=g(1)=1-a,有h(a)=a.综上所述,h(a)=
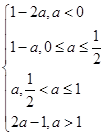
(2)画出y=h(x)的图象,如图所示,数形结合可得h(x)min=h(
 )=
)= .
.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立.  为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间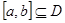 (其中
(其中 ),使得当
),使得当 时,
时,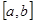 ,则称函数
,则称函数 是
是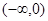 上的正函数,则实数
上的正函数,则实数 的取值范围为( )
的取值范围为( )





 ,则不等式f(x)>f(1)的解集是( )
,则不等式f(x)>f(1)的解集是( ) 上两个不同点处的切线重合,则称这条切线为曲线
上两个不同点处的切线重合,则称这条切线为曲线 ;②
;②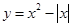 ;③
;③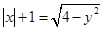 ;④
;④ 对应的曲线中存在“自公切线”的有( )
对应的曲线中存在“自公切线”的有( ) x ②f:x→y=
x ②f:x→y= x ③f:x→y=
x ③f:x→y= x ④f:x→y=x
x ④f:x→y=x