题目内容
若函数 为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间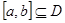 (其中
(其中 ),使得当
),使得当 时,
时, 的取值范围恰为
的取值范围恰为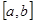 ,则称函数
,则称函数 是
是 上的正函数.若函数
上的正函数.若函数 是
是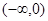 上的正函数,则实数
上的正函数,则实数 的取值范围为( )
的取值范围为( )
 为定义域
为定义域 上的单调函数,且存在区间
上的单调函数,且存在区间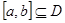 (其中
(其中 ),使得当
),使得当 时,
时, 的取值范围恰为
的取值范围恰为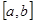 ,则称函数
,则称函数 是
是 上的正函数.若函数
上的正函数.若函数 是
是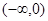 上的正函数,则实数
上的正函数,则实数 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
A
试题分析:根据二次函数的图像与性质可知函数
 在
在 单调递减,所以当
单调递减,所以当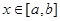 且
且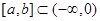 时,
时,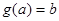 ,
,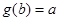 即
即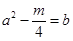 ,
,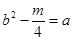 ,两式相减得
,两式相减得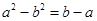 ,因为
,因为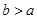 ,所以
,所以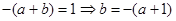 ,代入
,代入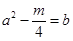 得
得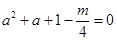 ,由
,由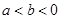 且
且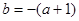 可得
可得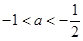 ,所以关于
,所以关于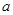 的二次方程
的二次方程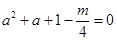 在区间
在区间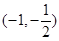 内有实数解,
内有实数解,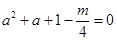 在区间
在区间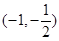 内有实数解又可转化为
内有实数解又可转化为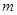 关于
关于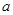 的函数
的函数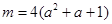 在区间
在区间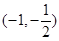 的值域,因为函数
的值域,因为函数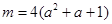 在
在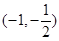 单调递减,所以
单调递减,所以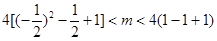 即
即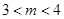 ,故选A.
,故选A.
练习册系列答案
相关题目
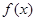 ,若存在实数对(
,若存在实数对(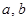 ),使得等式
),使得等式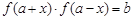 对定义域中的每一个
对定义域中的每一个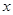 都成立,则称函数
都成立,则称函数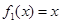 是否为 “(
是否为 “(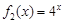 是“(
是“(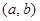 ;
;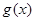 是“
是“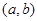 型函数”,对应的实数对
型函数”,对应的实数对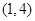 ,当
,当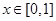 时,
时,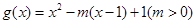 ,若当
,若当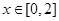 时,都有
时,都有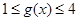 ,试求
,试求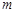 的取值范围.
的取值范围. ,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).





 的最小值是
的最小值是 ,且
,且 ,
, 求
求 的值:
的值: ,且
,且 在区间
在区间 恒成立,试求
恒成立,试求 取范围;
取范围;
 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.