题目内容
椭圆G:
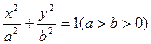 的两个焦点
的两个焦点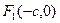 、
、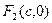 ,M是椭圆上一点,且满足
,M是椭圆上一点,且满足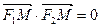 .
. (1)求离心率
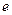 的取值范围;
的取值范围;(2)当离心率
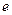 取得最小值时,点
取得最小值时,点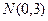 到椭圆上的点的最远距离为
到椭圆上的点的最远距离为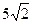 ;
;①求此时椭圆G的方程;
②设斜率为
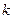 (
(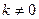 )的直线
)的直线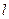 与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点
与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点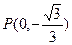 、Q的直线对称?若能,求出
、Q的直线对称?若能,求出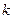 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.(1)
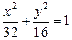
(2)
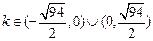
解:(1)离心率的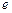 的取值范围是
的取值范围是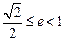 ;
;
(2)①当离心率的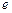 取最小值
取最小值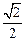 时,椭圆的方程可表示为
时,椭圆的方程可表示为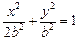 。
。
设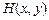 是椭圆上的一点,则
是椭圆上的一点,则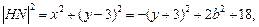 其中
其中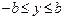 。
。
若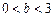 ,则当
,则当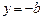 时,
时,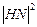 有最大值
有最大值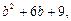 所以
所以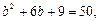 解得
解得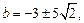 (均舍去)。
(均舍去)。
若 ,则当
,则当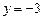 时,
时,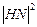 有最大值
有最大值 所以
所以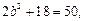 解得
解得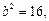
∴所求椭圆方程为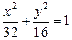 ;
;
②设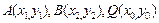 ,则由
,则由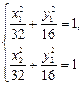 两式相减得
两式相减得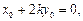 ……. ①
……. ①
又直线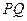 ⊥直线
⊥直线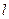 ∴直线
∴直线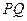 的方程为
的方程为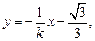 ,将
,将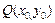 坐标代入得
坐标代入得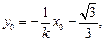 ……. ②
……. ②
由①②解得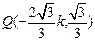 ,而点Q必在椭圆得内部,∴
,而点Q必在椭圆得内部,∴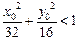 ,由此可得
,由此可得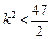 ,又
,又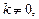 ∴
∴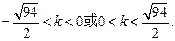
故当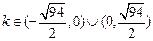 时,A,B两点关于过点P,Q得直线对称.)
时,A,B两点关于过点P,Q得直线对称.)
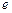 的取值范围是
的取值范围是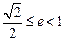 ;
; (2)①当离心率的
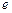 取最小值
取最小值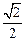 时,椭圆的方程可表示为
时,椭圆的方程可表示为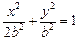 。
。设
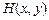 是椭圆上的一点,则
是椭圆上的一点,则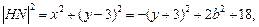 其中
其中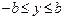 。
。若
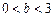 ,则当
,则当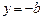 时,
时,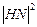 有最大值
有最大值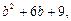 所以
所以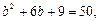 解得
解得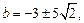 (均舍去)。
(均舍去)。若
 ,则当
,则当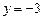 时,
时,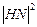 有最大值
有最大值 所以
所以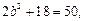 解得
解得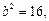
∴所求椭圆方程为
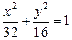 ;
; ②设
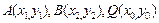 ,则由
,则由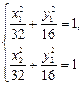 两式相减得
两式相减得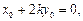 ……. ①
……. ①又直线
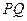 ⊥直线
⊥直线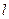 ∴直线
∴直线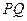 的方程为
的方程为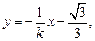 ,将
,将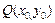 坐标代入得
坐标代入得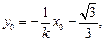 ……. ②
……. ②由①②解得
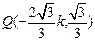 ,而点Q必在椭圆得内部,∴
,而点Q必在椭圆得内部,∴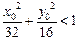 ,由此可得
,由此可得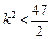 ,又
,又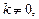 ∴
∴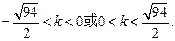
故当
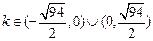 时,A,B两点关于过点P,Q得直线对称.)
时,A,B两点关于过点P,Q得直线对称.)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
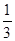
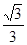
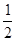
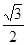
 (a>b>0)的离心率
(a>b>0)的离心率 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
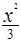 +
+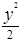 =1上一点P到左焦点的距离为
=1上一点P到左焦点的距离为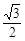 ,则P到右准线的距离为( )
,则P到右准线的距离为( )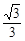
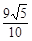

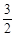
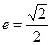 ,此椭圆与直线
,此椭圆与直线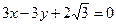 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).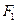 、
、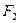 为椭圆的两个焦点,求
为椭圆的两个焦点,求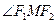 的取值范围;
的取值范围; 的方程为
的方程为 ,斜率为1的直线
,斜率为1的直线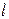 与椭圆
与椭圆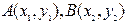 两点.
两点. ,直线
,直线 过点
过点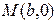 ,且
,且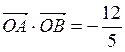 ,求椭圆
,求椭圆 的方程;
的方程; ,若点
,若点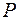 在椭圆
在椭圆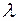 的取值范围.
的取值范围.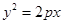 的焦点与椭圆
的焦点与椭圆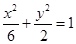 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )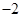
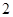
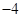
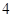
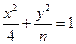 恒有两个交点,则
恒有两个交点,则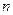 的取值范围____
的取值范围____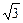 ),椭圆
),椭圆 +
+ 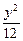 =1的右焦点为F,点P在椭圆上移动,当|PA|+2|PF|取最小值时,P点的坐标是__________.
=1的右焦点为F,点P在椭圆上移动,当|PA|+2|PF|取最小值时,P点的坐标是__________.