题目内容
甲、乙两校计划周末组织学生参加敬老活动,甲校每位同学往返车费是5元,每人可为3位老人服务,乙校每位同学往返车费是3元,每人可为5位老人服务.两校都有学生参加,甲校参加活动的学生比乙校至少多1人,且两校同学往返总车费不超过45元.如何安排甲、乙两校参加活动的人数,才能使受到服务的老人最多?受到服务的老人最多是多少?
设甲、乙两校参加活动的人数分别为x、y…(1分),
受到服务的老人的人数为z=3x+5y…(2分),
依题意,x、y应满足的约束条件为
…(6分)
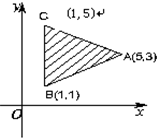
可行域为图中阴影部分中的整点,
画直线l0:3x+5y=0,并向右上方平移l0到l,当l经过可行域的某点,且可行域内其他点都在直线l的、包含直线l0的同一侧时,
这一点的坐标使目标函数取最大值…(7分)
 解方程组
解方程组
…(8分),
得
…(9分),M(6,5)满足约束条件,
因此,当x=6,y=5时,z取最大值…(10分)zmax=3×6+5×5=43…(11分).
答:甲、乙两校参加活动的人数分别为6和5时,受到服务的老人最多,最多为43人.…(12分)
受到服务的老人的人数为z=3x+5y…(2分),
依题意,x、y应满足的约束条件为
|
可行域为图中阴影部分中的整点,
画直线l0:3x+5y=0,并向右上方平移l0到l,当l经过可行域的某点,且可行域内其他点都在直线l的、包含直线l0的同一侧时,
这一点的坐标使目标函数取最大值…(7分)
 解方程组
解方程组
|
得
|
因此,当x=6,y=5时,z取最大值…(10分)zmax=3×6+5×5=43…(11分).
答:甲、乙两校参加活动的人数分别为6和5时,受到服务的老人最多,最多为43人.…(12分)

练习册系列答案
相关题目
 为三角形
为三角形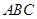 的三边,求证:
的三边,求证: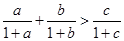
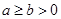 ,求证:
,求证: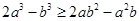 .
.
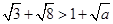 成立的正整数a的最大值是 ( )
成立的正整数a的最大值是 ( )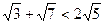 可选择的方法有以下几种,其中最合理的是 ( )
可选择的方法有以下几种,其中最合理的是 ( ) 