题目内容
设 为三角形
为三角形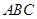 的三边,求证:
的三边,求证: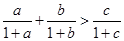
 为三角形
为三角形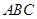 的三边,求证:
的三边,求证: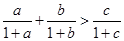
见解析
试题分析:本题用直接法不易找到证明思路,用分析法,要证该不等式成立,因为
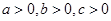 ,所以
,所以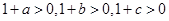 ,只需证该不等式两边同乘以
,只需证该不等式两边同乘以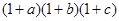 转化成的等价不等式a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)成立,用不等式性质整理为a+2ab+b+abc>c成立,用不等式性质及三角不等式很容易证明此不等式成立.
转化成的等价不等式a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)成立,用不等式性质整理为a+2ab+b+abc>c成立,用不等式性质及三角不等式很容易证明此不等式成立.试题解析:要证明:
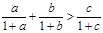
需证明: a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b) 5分
需证明:a(1+b+c+bc)+ b(1+a+c+ac)> c(1+a+b+ab) 需证明a+2ab+b+abc>c 10分
∵a,b,c是
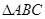 的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0 ∴a+2ab+b+abc>c
∴
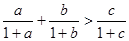 成立。 14分
成立。 14分
练习册系列答案
相关题目
 >
> ,x>y.
,x>y.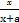 >
>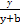 .
. 之间的大小关系是( )
之间的大小关系是( ) ,且
,且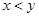 ,求证:
,求证:
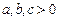 ,求证:
,求证: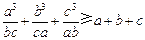 .
.