题目内容
【题目】已知函数f(x)= ![]() ﹣a是奇函数
﹣a是奇函数
(1)求实数a的值;
(2)判断函数在R上的单调性并用函数单调性的定义证明;
(3)对任意的实数x,不等式f(x)<m﹣1恒成立,求实数m的取值范围.
【答案】
(1)解:由f(x)是奇函数,有f(﹣x)=﹣f(x),
∴ ![]() ﹣a=﹣(
﹣a=﹣( ![]() ﹣a),
﹣a),
∴2a=1,∴a= ![]()
(2)解:f(x)= ![]() ﹣
﹣ ![]() ,f(x)在R上是增函数,
,f(x)在R上是增函数,
下证:设x1、x2∈R且x1<x2,且x1、x2是任意的,
f(x1)﹣f(x2)
=( ![]() ﹣
﹣ ![]() )﹣(
)﹣( ![]() ﹣
﹣ ![]() )
)
= ![]() ,
,
∵x1<x2,∴ ![]() <
< ![]() ,
,
∴ ![]() <0,
<0,
即f(x1)<f(x2),
∴f(x)在R上是增函数
(3)解:对任意的实数x,不等式f(x)<m﹣1恒成立,
则只需m﹣1>f(x)max,
∵3x+1>1,∴0< ![]() <1,
<1,
∴﹣1< ![]() <0,
<0,
﹣ ![]() <
< ![]() ﹣
﹣ ![]() <
< ![]() ,即﹣
,即﹣ ![]() <f(x)<
<f(x)< ![]() ,
,
∴m﹣1≥ ![]() ,∴m≥
,∴m≥ ![]() ,
,
即m的取值范围为:[ ![]() ,+∞)
,+∞)
【解析】(1)由奇函数定义知,有f(﹣x)=﹣f(x)恒成立,由此可求a值;(2)设x1、x2∈R且x1<x2 , 通过作差判断f(x2)与f(x1)的大小,利用函数单调性的定义可作出判断;(3)对任意的实数x,不等式f(x)>2m﹣1恒成立,等价于m﹣1>f(x)max , 根据基本函数的值域可求出f(x)max .
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.

 名师点睛字词句段篇系列答案
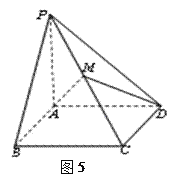
名师点睛字词句段篇系列答案【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润![]() 销售收入
销售收入![]() 成本)(附:对于一组数据
成本)(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: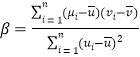 ,
,![]() ),
),![]() ,
,![]()