题目内容
设一部机器在一天内发生故障的概率为0
2，机器发生故障时全天停止工作 若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少？
2，机器发生故障时全天停止工作 若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少？故一周内的期望利润为5.216(万元)
以X表示一周5天内机器发生故障的天数，则X－B(5，0.2)，于是X有概率分布P(X=k)=C
0.2k0.85－k,k=0,1,2,3,4,5.
以Y表示一周内所获利润，则
Y=g(X)=
Y的概率分布为:
P(Y=10)=P(X=0)=0.85=0.328
P(Y=5)=P(X=1)=C
0.2·0.84=0.410
P(Y=0)=P(X=2)=C
·0.22·0.83=0.205
P(Y=－2)=P(X≥3)=1－P(X=0)－P(X=1)－P(X=2)=0.057
故一周内的期望利润为:
EY=10×0.328+5×0.410+0×0.205－2×0.057=5.216(万元)
0.2k0.85－k,k=0,1,2,3,4,5.以Y表示一周内所获利润，则
Y=g(X)=
Y的概率分布为:
P(Y=10)=P(X=0)=0.85=0.328
P(Y=5)=P(X=1)=C
0.2·0.84=0.410P(Y=0)=P(X=2)=C
·0.22·0.83=0.205P(Y=－2)=P(X≥3)=1－P(X=0)－P(X=1)－P(X=2)=0.057
故一周内的期望利润为:
EY=10×0.328+5×0.410+0×0.205－2×0.057=5.216(万元)
练习册系列答案
相关题目
，他们的投票相互没有影响．规定：若投票结果中至少有两张“同意”票，则决定对该项目投资；否则，放弃对该项目投资．
，求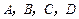
四个交通岗，其中在
岗遇到红灯的概率均为
，在
岗遇到红灯的概率均为
．假设他在4个交通岗遇到红灯的事件是相互独立的，X表示他遇到红灯的次数．
，就会迟到，求张华不迟到的概率；（2）求EX．
的概率分布列及数学期望。
是一个离散型随机变量，其分布列如下表：求
值，并求
．
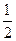
表示所选3人中的女生人数。写出
，用随机变量
表示A在1次实验中发生的次数。（1）求方差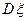
的最大值；（2）求
的最大值。
（各单位是否录用他相互独立，允许小明被多个单位同时录用） （1）求小明没有被录用的概率；（2）设录用小明的单位个数为
，求