题目内容
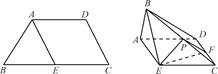
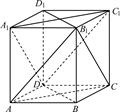
如图,在四棱锥PABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=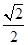 AD.若E、F分别为PC、BD的中点,求证:
AD.若E、F分别为PC、BD的中点,求证:
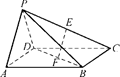
(1)EF∥平面PAD;
(2)EF⊥平面PDC.
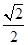 AD.若E、F分别为PC、BD的中点,求证:
AD.若E、F分别为PC、BD的中点,求证:
(1)EF∥平面PAD;
(2)EF⊥平面PDC.
(1)见解析(2)见解析
(1)连结AC,则F是AC的中点,在△CPA中,EF∥PA,且PA 平面PAD,EF
平面PAD,EF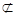 平面PAD,∴EF∥平面PAD.
平面PAD,∴EF∥平面PAD.
(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,∴CD⊥平面PAD,∴CD⊥PA.
又PA=PD=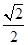 AD,∴△PAD是等腰直角三角形,且∠APD=
AD,∴△PAD是等腰直角三角形,且∠APD= ,即PA⊥PD,而CD∩PD=D,
,即PA⊥PD,而CD∩PD=D,
∴PA⊥平面PDC.又EF∥PA,∴EF⊥平面PDC.
 平面PAD,EF
平面PAD,EF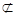 平面PAD,∴EF∥平面PAD.
平面PAD,∴EF∥平面PAD.(2)∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,∴CD⊥平面PAD,∴CD⊥PA.
又PA=PD=
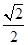 AD,∴△PAD是等腰直角三角形,且∠APD=
AD,∴△PAD是等腰直角三角形,且∠APD= ,即PA⊥PD,而CD∩PD=D,
,即PA⊥PD,而CD∩PD=D,∴PA⊥平面PDC.又EF∥PA,∴EF⊥平面PDC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
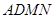 都为正方形,
都为正方形,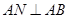 ,F
,F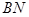 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.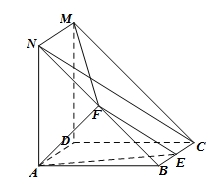
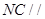 平面AEF;
平面AEF;
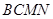 平面;
平面;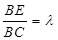 ,写出
,写出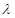 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明). A1B1C1,
A1B1C1,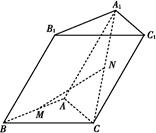



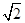 ,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)
,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)