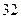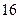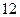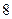题目内容
设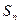 为数列
为数列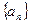 的前
的前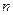 项和,已知
项和,已知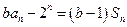
⑴证明:当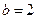 时,
时,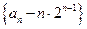 是等比数列;
是等比数列;
⑵求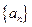 的通项公式
的通项公式
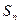 为数列
为数列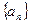 的前
的前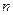 项和,已知
项和,已知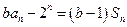
⑴证明:当
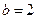 时,
时,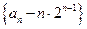 是等比数列;
是等比数列;⑵求
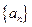 的通项公式
的通项公式⑴证明略⑵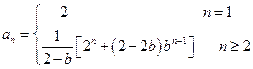
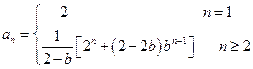
由递推公式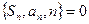 求数列的通项公式
求数列的通项公式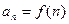 ,主要利用:
,主要利用:
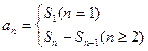 ,同时注意分类讨论思想.由题意知
,同时注意分类讨论思想.由题意知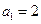 ,且
,且 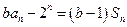 ,
,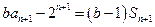
两式相减,得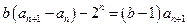 ,即
,即 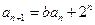 ①
①
⑴当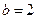 时,由①知
时,由①知 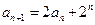
于是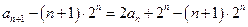
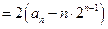
又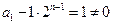 ,所以
,所以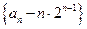 是首项为
是首项为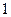 ,公比为
,公比为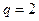 的等比数列。
的等比数列。
⑵当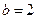 时,由(Ⅰ)知
时,由(Ⅰ)知 ,即
,即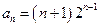
当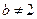 时,由①得
时,由①得 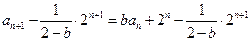
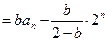
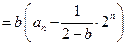
因此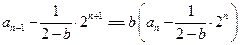
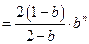
得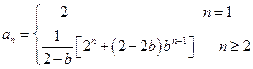
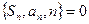 求数列的通项公式
求数列的通项公式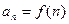 ,主要利用:
,主要利用: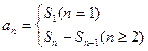 ,同时注意分类讨论思想.由题意知
,同时注意分类讨论思想.由题意知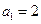 ,且
,且 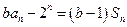 ,
,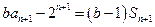
两式相减,得
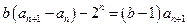 ,即
,即 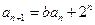 ①
①⑴当
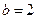 时,由①知
时,由①知 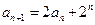
于是
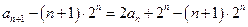
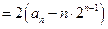
又
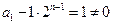 ,所以
,所以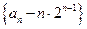 是首项为
是首项为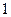 ,公比为
,公比为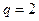 的等比数列。
的等比数列。⑵当
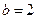 时,由(Ⅰ)知
时,由(Ⅰ)知 ,即
,即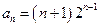
当
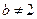 时,由①得
时,由①得 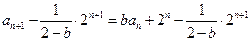
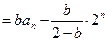
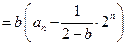
因此
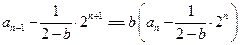
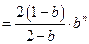
得
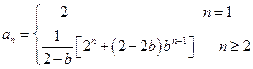

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
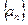 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈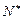 .
.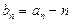 ,求证:数列
,求证:数列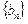 是等比数列;
是等比数列;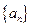 中,
中,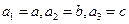 ,
,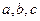 分别为
分别为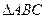 的三内角
的三内角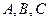 的对边,且
的对边,且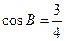 .
.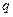 ;
;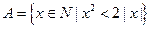 ,且
,且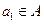 ,求数列
,求数列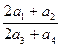 的值为( )
的值为( )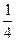
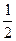
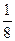
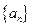 的前
的前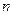 项和为
项和为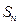 ,求证
,求证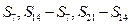 也成等比数列.
也成等比数列.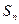 为等比数列
为等比数列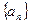 前
前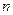 项和,
项和,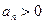 ,
,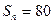 ,
,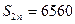 ,前
,前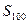 .
.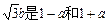 的等比中项,则a+3b的最大值为
的等比中项,则a+3b的最大值为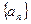 中,
中,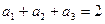 ,
, ,则
,则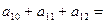 ( )
( )