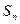题目内容
已知α,β,г成公比为2的等比数列,α∈[0,2π],且sinα,sinβ,sinг成等比数列。求α,β,г的值。
α=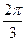 ,β=
,β=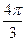 ,г=
,г=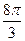 或α=
或α=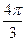 ,β=
,β=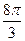 ,г=
,г=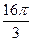
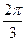 ,β=
,β=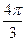 ,г=
,г=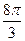 或α=
或α=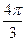 ,β=
,β=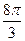 ,г=
,г=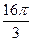
α,β,г成公比为2即β=2α,г=4α,
sinβ=sin2α=2sinαcosα,sinг=sin4α=2sin2αcos2α,
且sinα,sinβ,sinг成等比数列即sin2β=sinαsinг.
也即是sin22α=sinα×2sin2αcos2α,即sin2α=2sinαcos2α,即cosα=cos2α。
2cos2α-cosα-1=0,解得cosα=1或cosα=-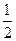 。
。
当cosα=1时,sinα=0与等比数列的项不为0矛盾。
当cosα=-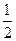 时,∵α∈[0,2π],∴α=
时,∵α∈[0,2π],∴α=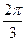 或
或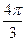 。
。
∴α=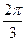 ,β=
,β=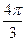 ,г=
,г=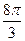 或α=
或α=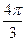 ,β=
,β=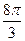 ,г=
,г=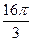 。
。
sinβ=sin2α=2sinαcosα,sinг=sin4α=2sin2αcos2α,
且sinα,sinβ,sinг成等比数列即sin2β=sinαsinг.
也即是sin22α=sinα×2sin2αcos2α,即sin2α=2sinαcos2α,即cosα=cos2α。
2cos2α-cosα-1=0,解得cosα=1或cosα=-
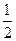 。
。当cosα=1时,sinα=0与等比数列的项不为0矛盾。
当cosα=-
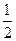 时,∵α∈[0,2π],∴α=
时,∵α∈[0,2π],∴α=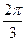 或
或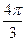 。
。∴α=
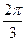 ,β=
,β=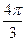 ,г=
,г=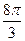 或α=
或α=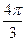 ,β=
,β=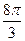 ,г=
,г=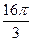 。
。
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
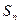 为数列
为数列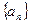 的前
的前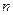 项和,已知
项和,已知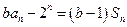
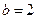 时,
时,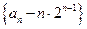 是等比数列;
是等比数列;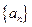 的通项公式
的通项公式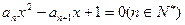 的两根
的两根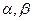 满足
满足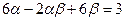 ,且
,且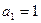
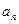 表示
表示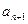 (2)求证:
(2)求证: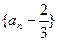 是等比数列
是等比数列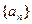 的前n项和
的前n项和