题目内容
【题目】在国家积极推动美丽乡村建设的政策背景下,各地根据当地生态资源打造了众多特色纷呈的乡村旅游胜地.某人意图将自己位于乡村旅游胜地的房子改造成民宿用于出租,在旅游淡季随机选取100天,对当地已有的六间不同价位的民宿进行跟踪,统计其出租率![]() (
(![]() ),设民宿租金为
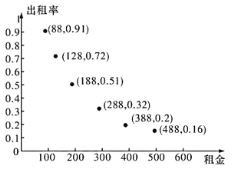
),设民宿租金为![]() (单位:元/日),得到如图所示的数据散点图.
(单位:元/日),得到如图所示的数据散点图.
(1)若用“出租率”近似估计旅游淡季民宿每天租出去的概率,求租金为388元的那间民宿在淡季内的三天中至少有2天闲置的概率.
(2)①根据散点图判断,![]() 与
与![]() 哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
哪个更适合于此模型(给出判断即可,不必说明理由)?根据判断结果求回归方程;
②若该地一年中旅游淡季约为280天,在此期间无论民宿是否出租,每天都要付出![]() 的固定成本,若民宿出租,则每天需要再付出
的固定成本,若民宿出租,则每天需要再付出![]() 的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益
的日常支出成本.试用①中模型进行分析,旅游淡季民宿租金约定为多少元时,该民宿在这280天的收益![]() 达到最大?
达到最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;![]() .
.
参考数据:记![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
【答案】(1)![]() (2)①
(2)①![]() 更适合,
更适合,![]() ②181元
②181元
【解析】
(1)三天中至少有2天闲置的即为3天中有两天闲置或者3天都闲置,又每天的出租率为0.2,根据二项分布的相关知识即可求出概率;
(2)①根据散点图的分布情况,各散点连线更贴近![]() 的图象,故
的图象,故![]() 的拟合效果更好,代入公式求出回归方程即可;②将收益表示为租金的函数,用函数单调性处理即可.
的拟合效果更好,代入公式求出回归方程即可;②将收益表示为租金的函数,用函数单调性处理即可.
(1)三天中至少有2天闲置的反面为3天中最多有一天能够租出,
又每天的出租率为0.2,
所以3天中至少有2天闲置的概率:
![]() .
.
(2)①根据散点图的分布情况,各散点连线更贴近![]() 的图象,
的图象,
故![]() 的拟合效果更好,
的拟合效果更好,
依题意,![]() ,
,![]() ,
,
所以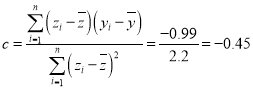 ,
,
所以![]() ,
,
所以回归方程为![]() .
.
②设旅游淡季民宿租金为![]() ,则淡季该民宿的出租率
,则淡季该民宿的出租率![]() ,
,
所以该民宿在这280天的收益:
![]()
![]() ,
,
所以![]() ,
,
令![]() 得,
得,![]() ,所以
,所以![]() ,
,
且当![]() 时
时![]() ,
,![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() 存在最大值,
存在最大值,
所以旅游淡季民宿租金约定为181元时,
该民宿在这280天的收益![]() 达到最大.
达到最大.

【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
某商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(2)求![]() 的分布列
的分布列
【题目】从某地区随机抽测120名成年女子的血清总蛋白含量(单位:![]() ),由测量结果得如图频数分布表:
),由测量结果得如图频数分布表:
(1)①仔细观察表中数据,算出该样本平均数![]() ______;
______;
②由表格可以认为,该地区成年女子的血清总蛋白含量Z服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本标准差s.经计算,该样本标准差
近似为样本标准差s.经计算,该样本标准差![]() .
.
医学上,Z过高或过低都为异常,Z的正常值范围通常取关于![]() 对称的区间
对称的区间![]() ,且Z位于该区间的概率为
,且Z位于该区间的概率为![]() ,试用该样本估计该地区血清总蛋白正常值范围.
,试用该样本估计该地区血清总蛋白正常值范围.
120名成年女人的血清总蛋白含量的频数分布表 | |||
分组 | 频数f | 区间中点值x |
|
| 2 | 65 | 130 |
| 8 | 67 | 536 |
| 12 | 69 | 828 |
| 15 | 71 | 1065 |
| 25 | 73 | 1825 |
| 24 | 75 | 1800 |
| 16 | 77 | 1232 |
| 10 | 79 | 790 |
| 7 | 81 | 567 |
| 1 | 83 | 83 |
合计 | 120 | 8856 | |
(2)结合(1)中的正常值范围,若该地区有5名成年女子检测血清总蛋白含量,测得数据分别为83.2,80,73,59.5,77,从中随机抽取2名女子,设血清总蛋白含量不在正常值范围的人数为X,求X的分布列和数学期望.
附:若![]() ,则
,则![]() .
.