题目内容
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,C的准线与E交于P,Q两点,且
的右焦点,C的准线与E交于P,Q两点,且![]() .
.
(1)求E的方程;
(2)过E的左顶点A作直线l交E于另一点B,且BO(O为坐标原点)的延长线交E于点M,若直线AM的斜率为1,求l的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,先得到椭圆焦点坐标,再由![]() ,得到
,得到![]() ,根据焦点坐标得到
,根据焦点坐标得到![]() ,两式联立,求出
,两式联立,求出![]() ,
,![]() ,即可得出结果;
,即可得出结果;
(2)先由题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立直线与椭圆方程,求出点
,联立直线与椭圆方程,求出点![]() 坐标,根据对称性,得到
坐标,根据对称性,得到![]() 的坐标,再由直线斜率公式,即可求出结果.
的坐标,再由直线斜率公式,即可求出结果.
(1)因为抛物线![]() 的焦点为
的焦点为![]() ,
,
由题意,可得:椭圆![]() 的两焦点为
的两焦点为![]() ,
,
又抛物线![]() 的准线与
的准线与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,将
,将![]() 代入椭圆方程得
代入椭圆方程得![]() ,所以
,所以![]() ,则
,则![]() ,即
,即![]() ①,
①,
又![]() ②,根据①②解得:
②,根据①②解得:![]() ,
,![]() ,
,
因此椭圆![]() 的方程为
的方程为![]() ;
;
(2)由(1)得![]() 的左顶点为
的左顶点为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
由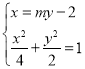 得
得![]() ,所以
,所以![]() ,
,
因此![]() ,所以
,所以![]() ,
,
则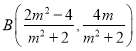 ,
,
又因为![]() (
(![]() 为坐标原点)的延长线交
为坐标原点)的延长线交![]() 于点
于点![]() ,
,
则![]() 与
与![]() 关于原点对称,所以
关于原点对称,所以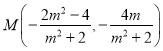 ,
,
因为直线![]() 的斜率为1,
的斜率为1,
所以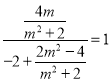 ,解得:
,解得:![]() ,
,
因此,直线![]() 的方程为:
的方程为:![]() .
.

练习册系列答案
相关题目